Random noise attenuation using local signal-and-noise orthogonalization

Appendix A: Signal-and-noise orthogonalization

demo
Figure 12. Demonstration of signal-and-noise orthogonalization.

As shown schematically in Figure A-1, the initially estimated signal and noise are denoted by $\mathbf{s}_0$ and $\mathbf{n}_0$ , respectively. By projecting $\mathbf{n}_0$ to the direction of $\mathbf{s}_0$ , we can get the projection $w\mathbf{s}_0$ . The other component of $\mathbf{n}_0$ is the final estimated noise, as shown in equation 3. The final estimated signal is thus the summation of the initially estimated signal $\mathbf{s}_0$ and the projection component $w\mathbf{s}_0$ .

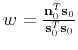When $w=\frac{\mathbf{n}_0^T\mathbf{s}_0}{\mathbf{s}_0^T\mathbf{s}_0}$ , the following equation holds:

$$\begin{split}\hat{\mathbf{n}}^T\hat{\mathbf{s}} &=(\mathbf{n}... ...\mathbf{s}_0}\right)^2\mathbf{s}_0^T\mathbf{s}_0 =0 \end{split}$$ (12)

Here, $\hat{\mathbf{s}}$ and $\hat{\mathbf{n}}$ denote the final estimated signal and noise, respectively, and appear orthogonal to each other. This orthogonalization approach is also known as Gram-Schmidt orthogonalization (Hazewinkel, 2001). Note that $w$ defined above can be obtained by solving the least-squares optimization problem:

$$\min_{w} \Arrowvert w\mathbf{s}_0-\mathbf{n}_0\Arrowvert^2_2,$$ (13)

which we extend to equation 7 in the main text.

Random noise attenuation using local signal-and-noise orthogonalization