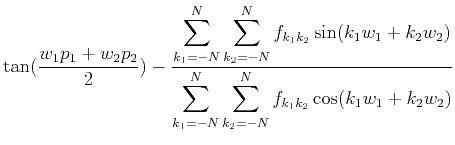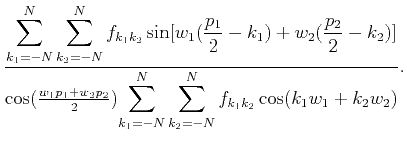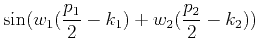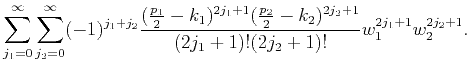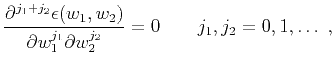|
 |
 |
 | Omnidirectional plane-wave destruction |  |
![[pdf]](icons/pdf.png) |
Next: Additional constraint
Up: 2D linear phase approximation
Previous: 2D linear phase approximation
The frequency response of the objective phase shift operator is
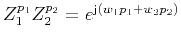 ,
where,
,
where, 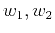 are frequencies in radius
in vertical and horizontal directions.
We must design the coefficients
are frequencies in radius
in vertical and horizontal directions.
We must design the coefficients
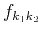 so that
the allpass system
so that
the allpass system
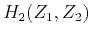 can obtain a similar linear phase response.
The frequency response of
can obtain a similar linear phase response.
The frequency response of
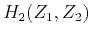 is
is
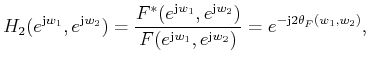 |
(8) |
where
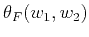 is the phase of
is the phase of
 ,
which takes the following form:
,
which takes the following form:
 |
(9) |
The phase approximating error is
 .
In order to obtain an analytical
.
In order to obtain an analytical
 ,
we remove
,
we remove 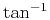 and redefine the phase approximating error as
and redefine the phase approximating error as
The sine function in the numerator can be expressed by
2D Taylor's expansion as
We use the maxflat phase criterion
(Thiran, 1971),
which means that the filter has a phase response
as flat as the desired linear response.
In the 2D case, the criterion
is equivalent to the mathematical expression that
the partial derivatives of the error function should be as small as possible.
We set them to be zero:
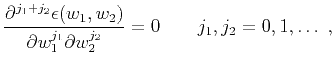 |
(11) |
which is equivalent to the following 2D maxflat condition:
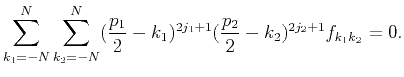 |
(12) |
 |
 |
 |
 | Omnidirectional plane-wave destruction |  |
![[pdf]](icons/pdf.png) |
Next: Additional constraint
Up: 2D linear phase approximation
Previous: 2D linear phase approximation
2013-08-09
![]() ,
where,
,
where, ![]() are frequencies in radius
in vertical and horizontal directions.
We must design the coefficients
are frequencies in radius
in vertical and horizontal directions.
We must design the coefficients
![]() so that
the allpass system
so that
the allpass system
![]() can obtain a similar linear phase response.
The frequency response of
can obtain a similar linear phase response.
The frequency response of
![]() is
is
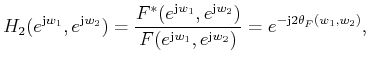
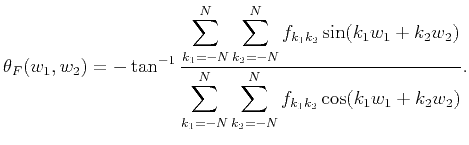
![]() .
In order to obtain an analytical
.
In order to obtain an analytical
![]() ,
we remove
,
we remove ![]() and redefine the phase approximating error as
and redefine the phase approximating error as