Selecting an optimal aperture in Kirchhoff migration using dip-angle images

Synthetic data examples

We next tested the presented approach on prestack migration of the Sigsbee2B data set (Paffenholz et al., 2002). The model contains a number of artificial point scatterers. The top of the salt body has a high curvature that acts as a transition between reflections and diffractions. There is a number of faults, which produce diffraction energy as well. Therefore, the data set is appropriate for testing of diffraction protection.

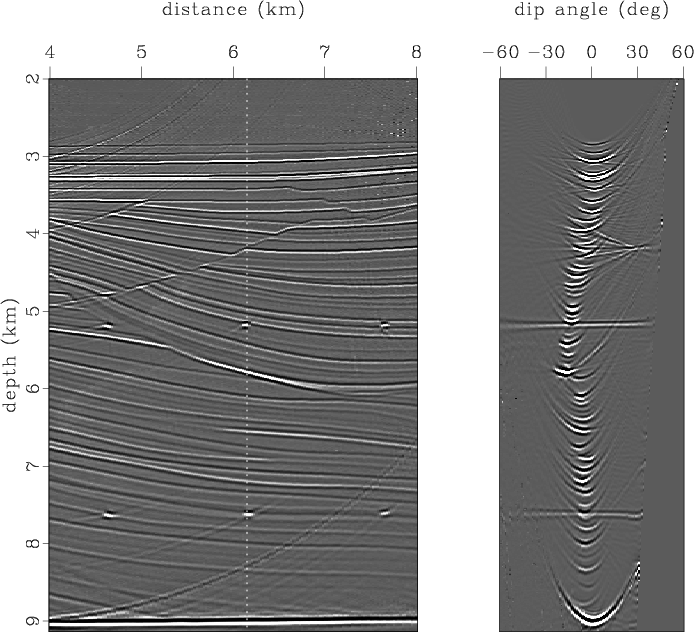
Figure 16 shows a seismic image of the left part of the model and one dip-angle gather extracted from the position in which two strong diffraction points are present. The gather contains two flat diffraction events at depths of 5.2 and 7.6 km, which correspond to the artificial scatterers. Some diffraction energy is also found at a depth of 4.3 km scattered by the fault.

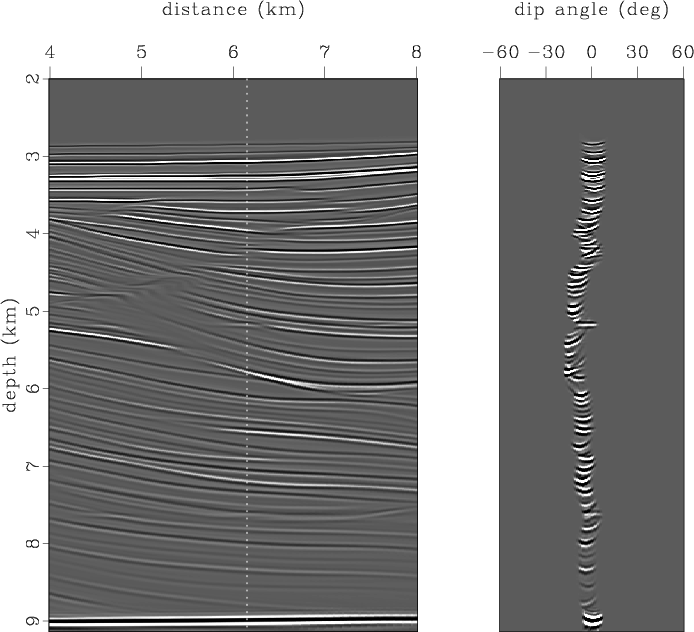
Figure 17 shows the image and dip-angle gather after migration-aperture limiting. First, we detected reflection apex positions, estimated effective dip ranges around them, and rejected migrated amplitudes that did not correspond to effective dip intervals. This procedure enables elimination of migration noise with correct imaging of reflection boundaries (Bienati et al., 2009). However, aperture limiting causes significant shortening of diffraction events and, as a result, weakening, or even disappearance, of diffraction objects in the image.

To optimize the migration aperture using the proposed slope-consistency approach, we performed semblance analysis using a dip-angle aperture of 10 degrees , a lateral base of 200 m, and parameters $s_1$ and $s_2$ equal to 0.2 and 0.4, respectively. (Figure 18). Reflection events become limited to the vicinity of their apexes, as in the previous example. At the same time, the procedure protects diffraction events in the gather and, hence, the corresponding diffraction objects in the image. Artificial point scatterers and faults are imaged correctly.

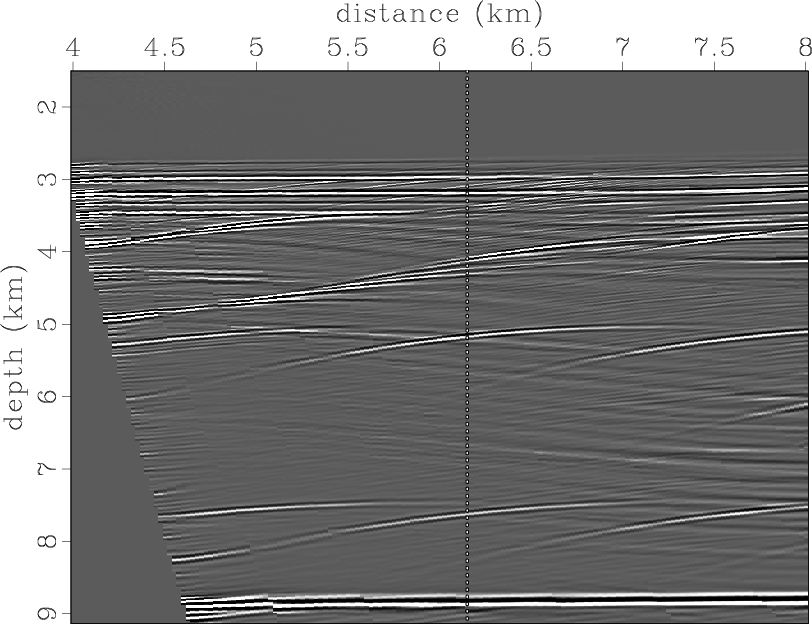
Figure 19a demonstrates one constant-dip partial image corresponding to 15 degrees. It resembles the seismic image of the model, with some differences. As expected, dipping reflection boundaries are shifted from the correct positions and diffraction objects are represented by hyperbolic events. After slope-consistency analysis, we construct a filtering mask (Figure 19b) to protect events whose slope is close to that of the dip of the partial image (Figure 19c). As a result, diffraction hyperbolas became confined to the vicinities of their correct positions, where they have the appropriate slope. Faults at a depth of 4 km and other reflection boundaries were protected as well. Remaining migrated energy was eliminated significantly.

sigs-input
Figure 16. Initial image and common-image gather in dip-angle domain corresponding to distance of 6.1 km.

sigs-ap
Figure 17. Image and dip-angle gather after migration-aperture limiting.

sigs-semb
Figure 18. Image and dip-angle gather after migration-aperture optimization by slope-consistency analysis.

pimage15-input-l,pimage15-mask,pimage15-semb-l
Figure 19. (a) Fifteen-degree constant-dip partial image, (b) weight function produced by slope-consistency analysis, and (c) partial image after migration-aperture optimization. Dashed line indicates position of considered artificial scattering points.

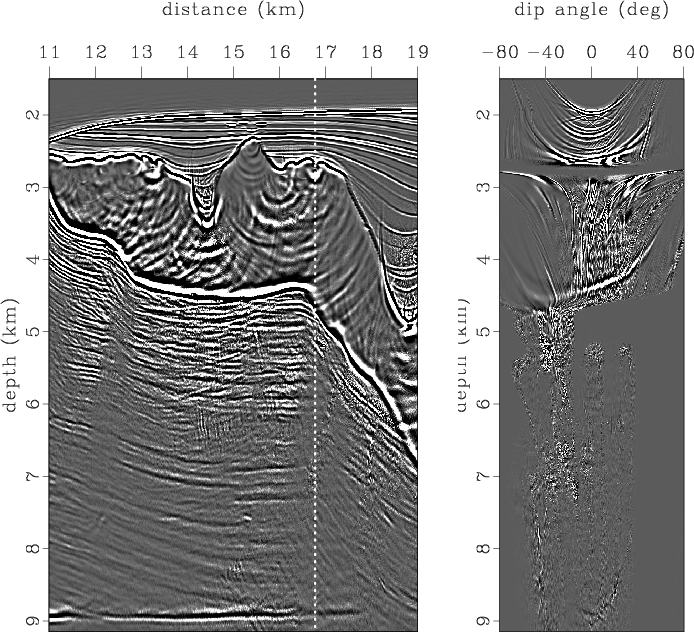
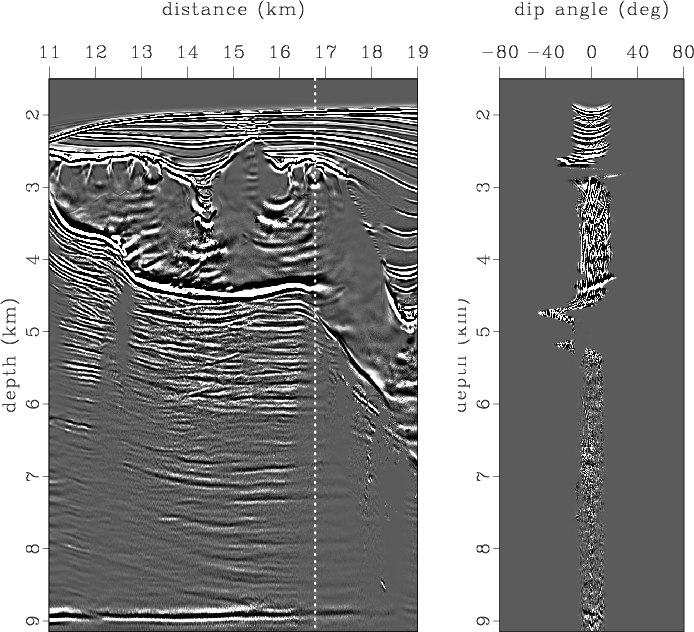
The salt body complicates Kirchhoff imaging in the right part of the Sigsbee model and increases the amount of migration noise. Figure 20 shows a seismic image and one dip-angle gather extracted from the position in which strong diffraction points are present. The scatterer at 7.6 km is illuminated well, and the dip-angle gather contains the corresponding plane diffraction event. A fault can be identified at the 15-km position and depth of 7 km. Some amount of migration noise is concentrated just below the salt and in the salt cavities above.

Migration-aperture optimization by slope-consistency analysis allows us to significantly decrease migration noise and, at the same time, to protect diffraction objects -- artificial point scatterers, the fault, and the salt boundary are all imaged correctly (Figure 21). In comparison, simple aperture limiting leads to noise suppression as well; however, the diffraction objects are lost, and the salt body appears distorted (Figure 22).

init
Figure 20. Initial image and common-image gather in dip-angle domain corresponding to distance of 16.8 km.

sca
Figure 21. Image and dip-angle gather after migration-aperture optimization by slope-consistency analysis.

ap
Figure 22. Image and dip-angle gather after migration-aperture limiting.

Selecting an optimal aperture in Kirchhoff migration using dip-angle images