Selecting an optimal aperture in Kirchhoff migration using dip-angle images

Diffractions and reflections in constant-dip partial images

Common-reflection-angle migration (Xu et al., 2001) can produce a set of dip-angle gathers in which traces are partial images of a fixed lateral position for different migration dips. At the same time, the migrated volume can be considered as a set of constant-dip partial images. Integration of the partial images along the dip angle provides a seismic image:

$$I(\mathbf{\bar{x}},z)=\int\limits\hat{I}(\mathbf{\bar{x}},z,\alpha)d\alpha\;,$$ (1)

where $\hat{I}(\mathbf{\bar{x}},z,\alpha)$ is a true-amplitude partial image for migration dip $\alpha$ (Bleistein and Gray, 2002).

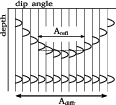
A dip-angle gather exposes the difference between reflections and diffractions (Landa et al., 2008; Audebert et al., 2002; Klokov and Fomel, 2012). Reflection events have a concave shape, and an image of a reflection boundary is constructed by a limited range of dip angles near the event apex. The effective range contains migrated impulses whose shift from the event apex does not exceed half the prevailing period. This area is equivalent to the Fresnel zone in the dip-angle domain. Diffraction events appear flat, however, which means that the full range of migration-dip angles provides an effective contribution to the image (Figure 1). Thus, an optimal migration aperture should simultaneously be limited for reflections and expanded for diffractions.

smile
Figure 1. Reflection event and diffraction event in the 2D dip-angle gather.

In the constant-dip partial-image domain, reflections and diffractions appear different as well, although they have some analogous features. To examine this, let us start with the simple case of zero-offset migration having the correct constant velocity. Similar derivations can be considered for prestack data.

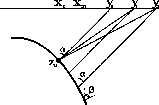
A diffraction event behaves hyperbolically (Figure 2a). Its shape is defined by the following equation (see derivation in Appendix):

$$z(x_m)=(x_m - x_0) \tan \alpha + \sqrt {(x_m - x_0)^2 / \cos^2 \alpha + z^2_0}\;,$$ (2)

where $\alpha$ is the constant-dip of the partial image, $x_m$ is an imaging position, and $x_0$ and $z_0$ are position and real depth of the diffraction point, respectively.

At the position of the diffraction point, when $x_m = x_0$, the event has the correct depth $z(x_m)=z_0$. The slope of the event at this point corresponds to the derivative:

$$\frac {\partial z }{\partial x_m} \vert_{x_m=x_0} = \tan \alpha\;.$$ (3)

Equation 3 indicates that an effective part of a diffraction event, which corresponds to the correct position and contributes to the image, has the same slope as the migration dip, or the constant-dip of the corresponding partial image.

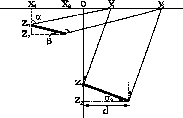
The response of a plane reflector in the constant-dip partial image is a segment. Let us consider a small part of the reflection boundary, which has a dip $\alpha_0$ and lateral length $d$ (Figure 2b). In the correct-constant-velocity case, coordinates of the segment edges after constant-dip migration can be defined by rotation around escape points $y_1$ and $y_2$:

$$\bar{x_1} = z_1 \frac{\sin \alpha_0 - \sin \alpha}{\cos \alpha_0}\;,$$ (4)

$$\bar{z_1} = z_1 \frac{\cos \alpha}{\cos \alpha_0}\;,$$ (5)

and

$$\bar{x_2} = z_2 \frac{\sin \alpha_0 - \sin \alpha}{\cos \alpha_0} + d\;,$$ (6)

$$\bar{z_2} = z_2 \frac{\cos \alpha}{\cos \alpha_0}\;.$$ (7)

The migrated edge points define a segment, whose slope is

$$\tan \beta = \frac {\bar{z_2}-\bar{z_1}}{\bar{x_2} - \bar{x_... ...c{\cos \alpha \sin \alpha_0}{1 - \sin \alpha \sin \alpha_0}\;.$$ (8)

Equation 8 illustrates some features of the migrated reflection boundary. For instance, a migrated horizontal reflector ($\alpha_0 = 0$) keeps the zero-slope independent of the migration dip.

scheme-diffr,scheme-refl
Figure 2. Constant-dip migration (scheme) of (a) a diffraction point and (b) a reflection boundary.

Equation 8 also allows us to find the condition in which the migrated slope is consistent with the constant-dip partial image ($\beta=\alpha$). In this case,

$$\frac{\cos \alpha \sin \alpha_0}{1 - \sin \alpha \sin \alpha_0} = \frac {\sin \alpha}{\cos \alpha}\;.$$ (9)

If $\alpha$ is derived from equation 9, note that the equation has only an $\alpha=\alpha_0$ solution. In other words, the slope of a migrated reflection event equals that of the migration dip only after migration with the correct dip. Such is the case when the segment corresponds to the stationary point and contributes to the image. Thus, an effective reflection event is consistent with the constant-dip partial image, as it is for diffractions. The derivation in the Appendix shows that this fact is true for curved reflectors as well.

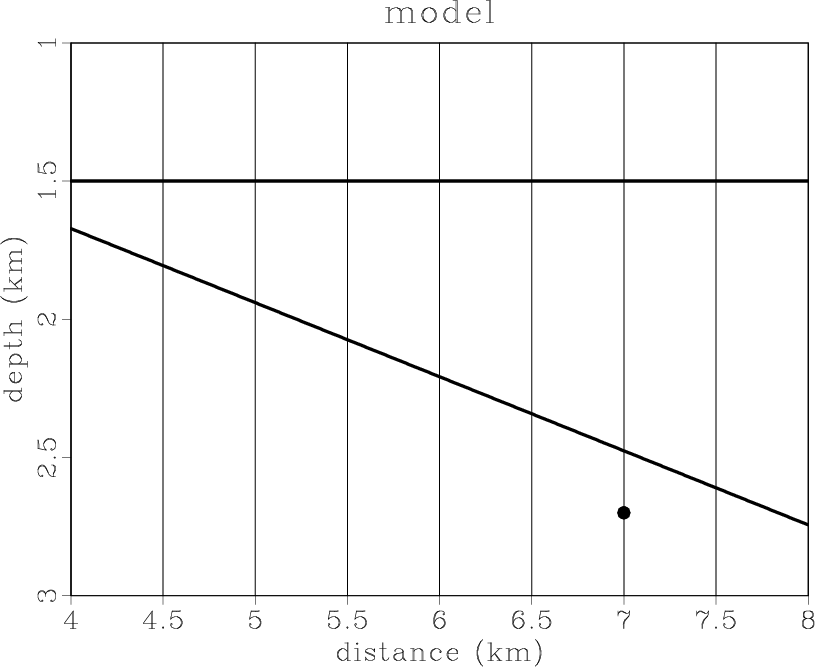
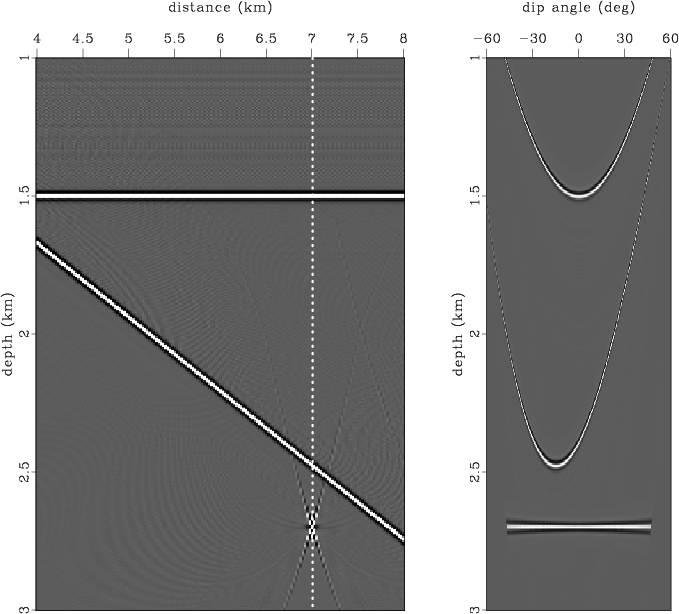
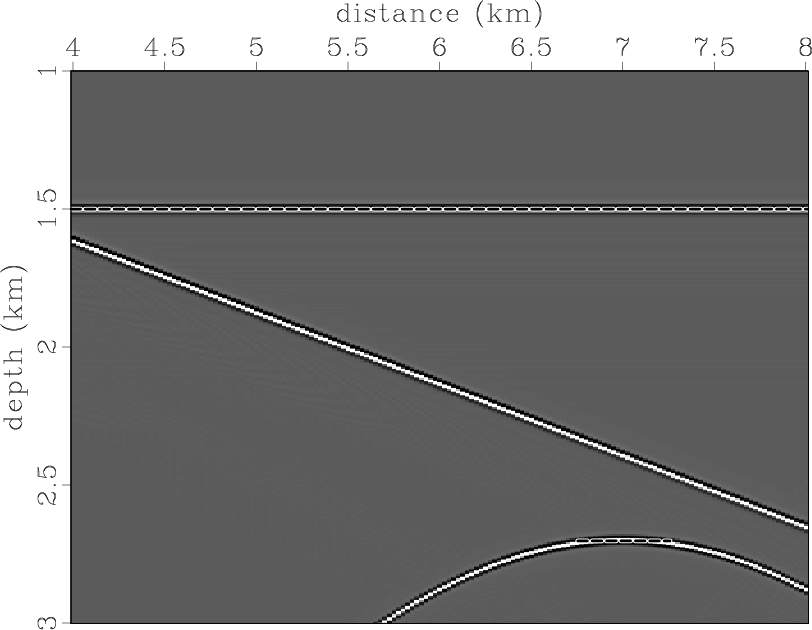
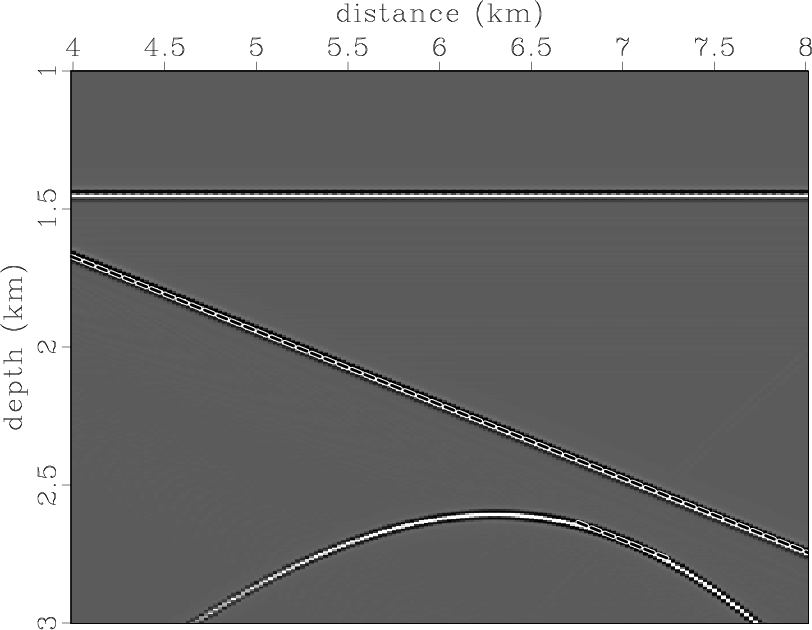
To verify the assertions presented, we ran the following experiment. We put two reflectors and one scattering point in the constant-velocity field (Figure 3). One reflector is flat, and the second has a dip of 15 degrees. We assume that reflectivity is generated by density variations. The modeled zero-offset section is presented in Figure 4. We migrated the data using Kirchhoff common-angle migration with the correct velocity. Figure 5 displays the image and a dip-angle gather extracted from the position where the scattering point is located. The diffraction event appears flat in the dip-angle gather, as expected, while the reflection events have concave shapes. Figure 6 shows two partial images corresponding to 0 and 15 degrees. Note that reflection boundaries and an effective part of the diffraction event are consistent with the partial image -- 0 and 15 degrees, respectively (the slope is indicated by dashed lines).

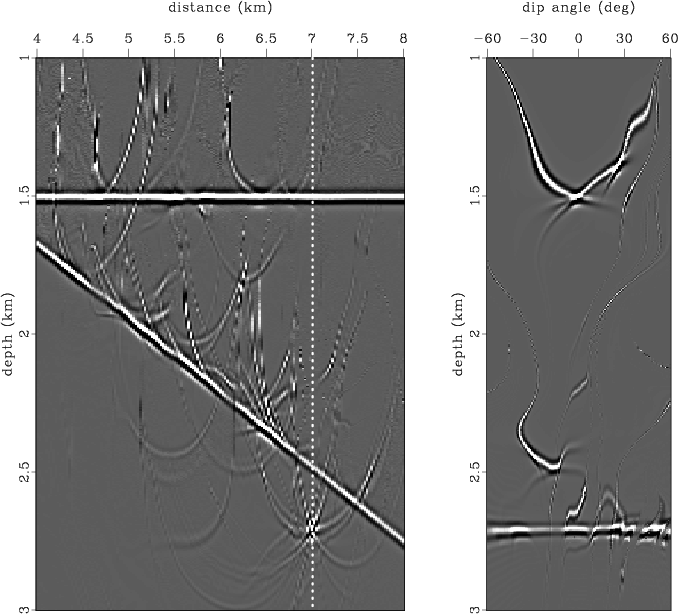
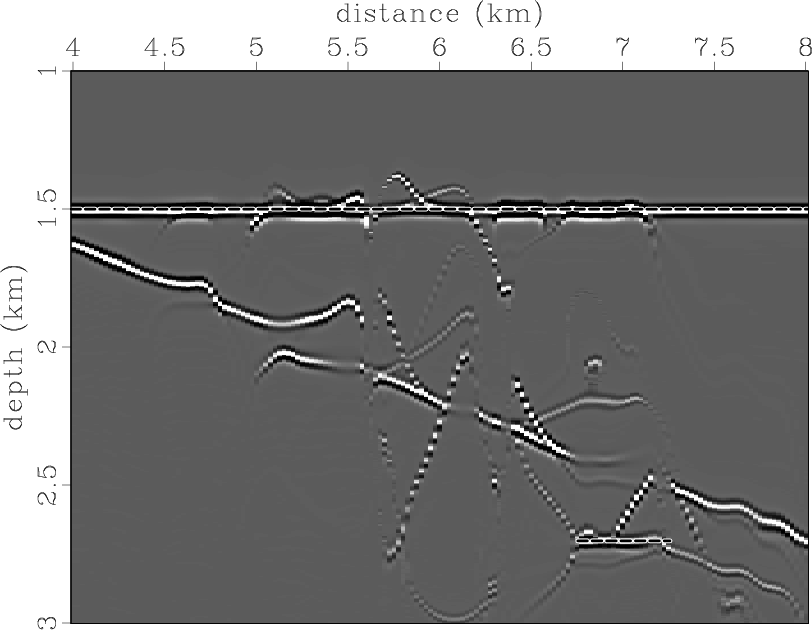
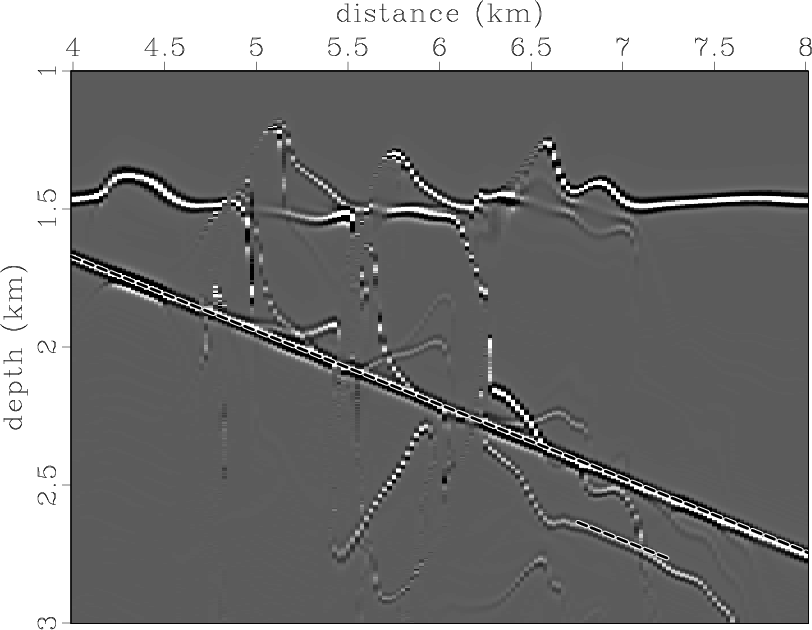
To represent a realistic situation, we placed the same reflectors and scattering point within a smoothed velocity field from the Marmousi model. Both reflection and diffraction events have complicated shapes in the data domain (Figure 7). Figure 8 displays the image and the dip-angle gather after migration with the correct velocity. The traveltimes for Kirchhoff angle-domain migration were computed by Huygens wavefront-tracing (Sava and Fomel, 2001), which allowed us to handle multiple arrivals. The diffraction event is flat, as it was in the constant-velocity example, but the shape of the reflection events appears much more complicated. The gather is contaminated by strong migration artifacts that produce noise in the image. Figure 9 shows two partial images corresponding to 0 and 15 degrees. Both images appear to be quite noisy. However, note that, even after migration with a complicated-velocity model, effective reflection events are consistent with the dips of partial images. The diffraction event at the scattering-point position has the appropriate slope as well (the slopes are indicated by dashed lines).

An event-slope-consistency analysis may provide information about separation between constructive and nonconstructive parts of migrated data. The key observation is that constructive reflection and diffraction events have slopes that are close to the constant-dip of the partial image. Slopes of nonconstructive events differ significantly from those of partial-image dips. Integration of constructive events only corresponds to migration having an optimal aperture.

theo-model
Figure 3. Theoretical model with two plane reflectors and one diffractor.

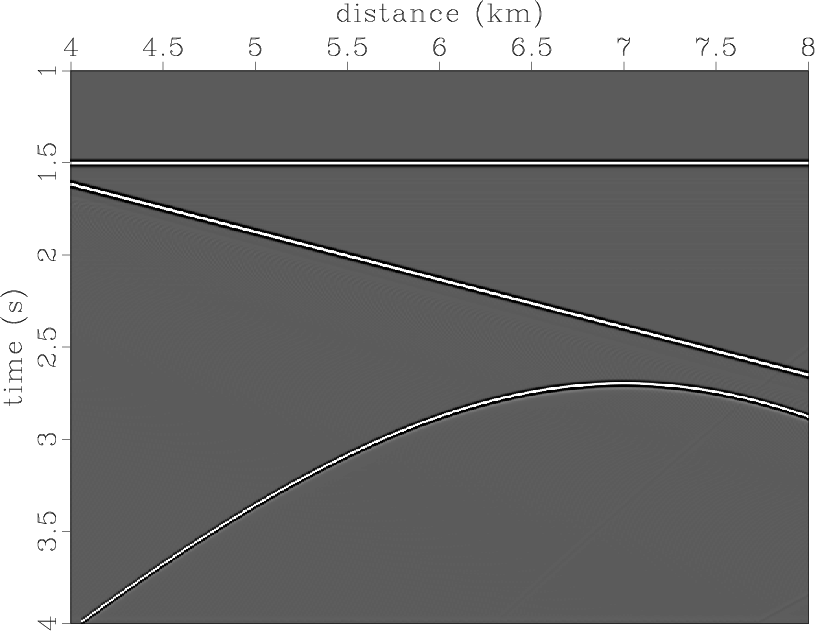
data0
Figure 4. Zero-offset section corresponding to the constant-velocity model.

zo-res-init
Figure 5. Depth-migrated image and common-image-gather in dip-angle domain corresponding to distance of 7 km.

zodpis0,zodpis15
Figure 6. (a) Zero-degree partial image and (b) fifteen-degree partial image for the constant-velocity model.

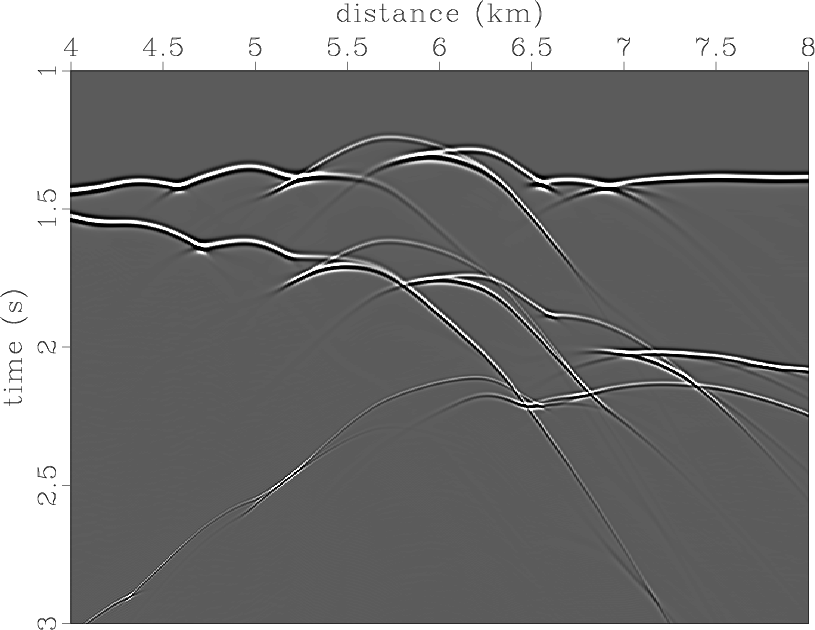
dm-zo
Figure 7. Zero-offset section corresponding to the Marmousi-velocity model.

res-init
Figure 8. Depth-migrated image and common-image-gather in dip-angle domain corresponding to distance of 7 km.

dpis0,dpis15
Figure 9. (a) Zero-degree partial image and (b) fifteen-degree partial image for the Marmousi-velocity model.

Selecting an optimal aperture in Kirchhoff migration using dip-angle images