|
|
|
|
Lowrank one-step wave extrapolation for reverse-time migration |


|
|---|
|
twolayer,fwavefd,wave1-2,wave2-2,wave1-3,wave2-3,wave1-10,wave1-20,wave1-30
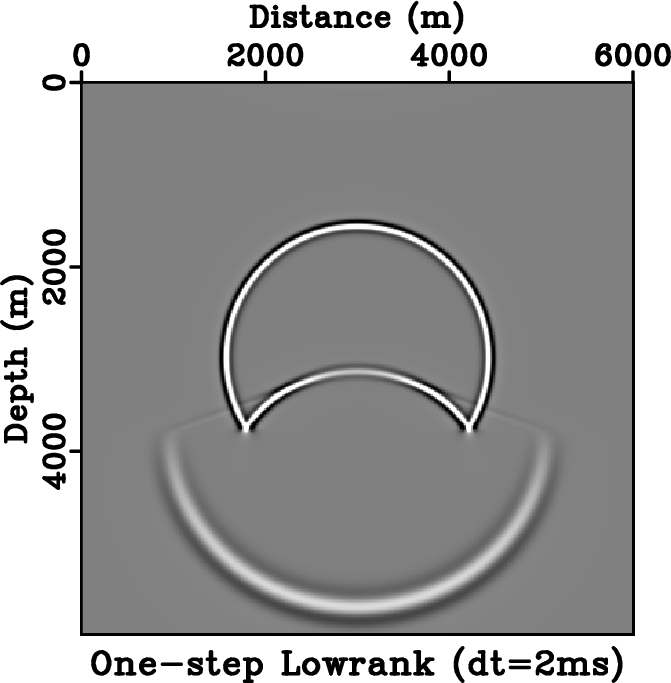
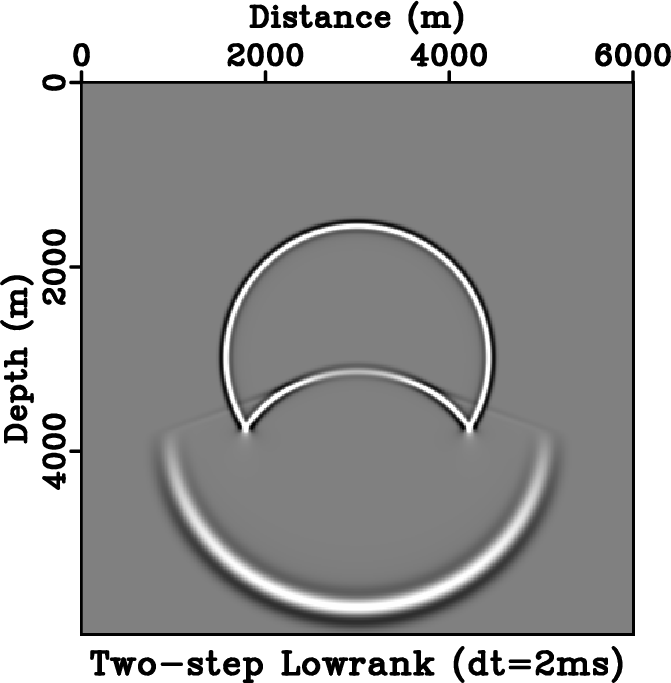
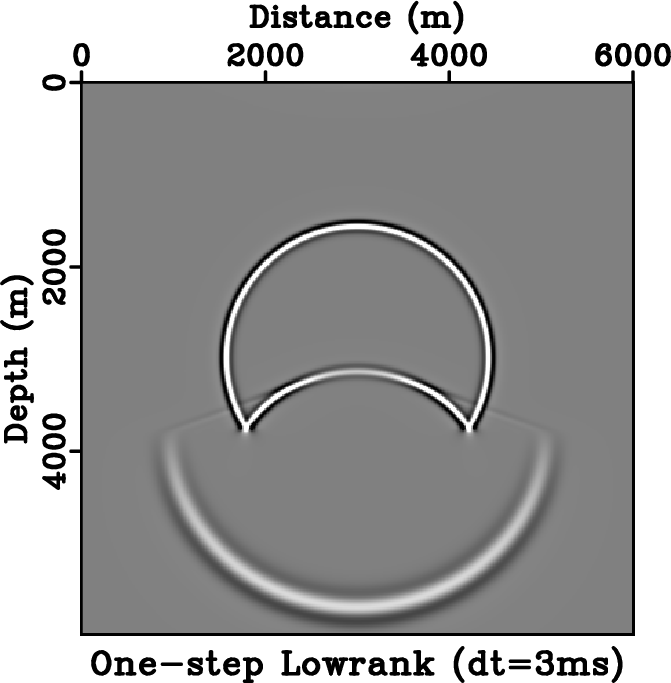
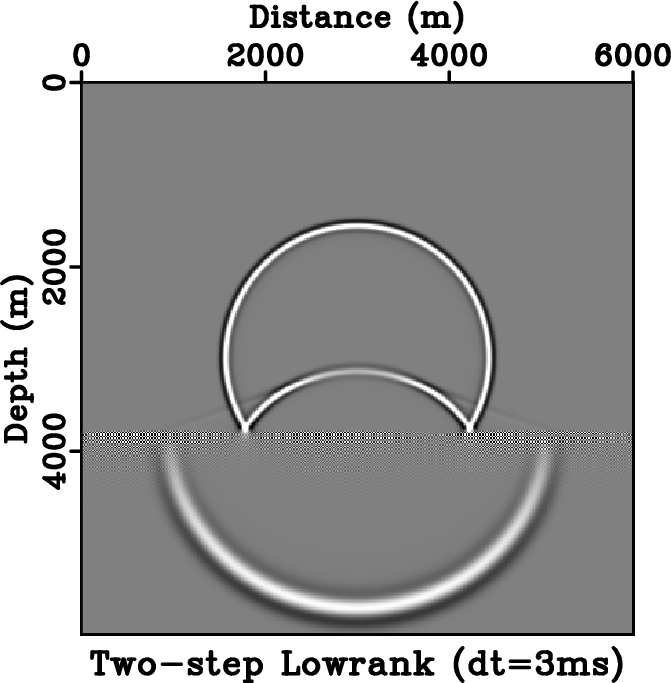
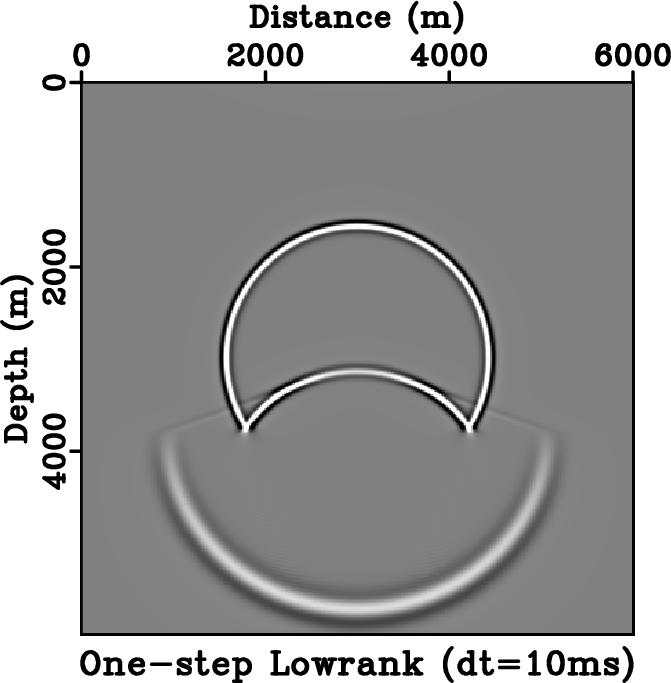
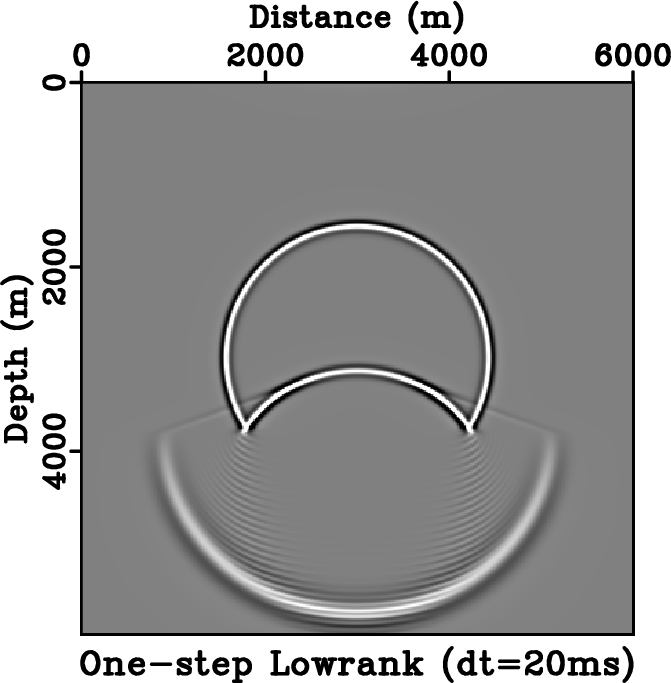
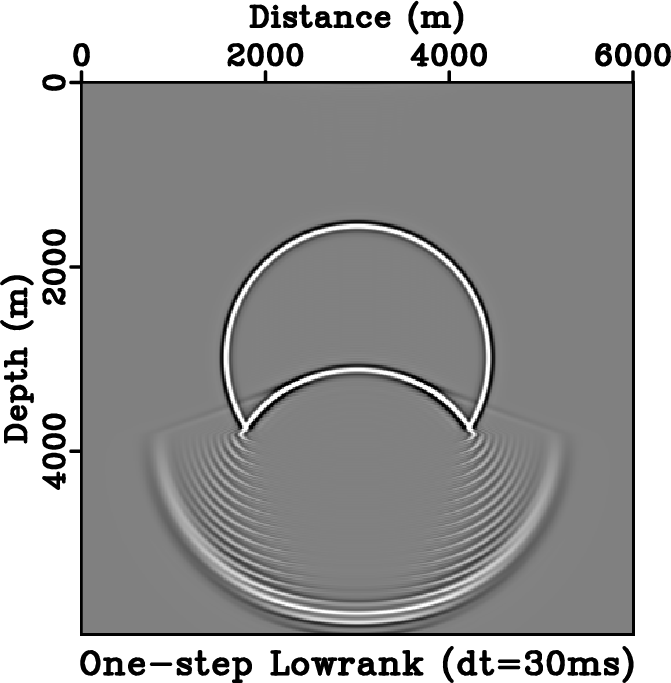
Figure 5. Stability comparison between different schemes. Wavefield snapshots are taken at |
|
|
We use a simple two-layer velocity model similar to the one used by Du et al. (2014) to demonstrate the stability of one-step wave extrapolation using lowrank approximation. Figure 5 shows the comparison among the stability of lowrank one-step, lowrank two-step and fourth-order FD methods. The velocity model has a sharp contrast at the depth of ![]() ; the upper layer has a velocity of
; the upper layer has a velocity of ![]() , and the lower layer has a velocity of
, and the lower layer has a velocity of ![]() (Figure 5a). The model is discretized on a
(Figure 5a). The model is discretized on a
![]() grid with a spacing of
grid with a spacing of ![]() along both horizontal and vertical directions. An explosive source, with a Ricker wavelet using a peak frequency of
along both horizontal and vertical directions. An explosive source, with a Ricker wavelet using a peak frequency of ![]() (maximum frequency approximately
(maximum frequency approximately ![]() ) is injected in the center of the model. When a time step of
) is injected in the center of the model. When a time step of ![]() is used, the classic fourth-order FD method suffers from visible dispersion artifacts (Figure 5b), whereas both the one-step and two-step schemes produce waves free of artifacts (Figure 5c and 5d). When a time step of
is used, the classic fourth-order FD method suffers from visible dispersion artifacts (Figure 5b), whereas both the one-step and two-step schemes produce waves free of artifacts (Figure 5c and 5d). When a time step of ![]() is used, the one-step scheme is stable (Figure 5e) whereas the two-step scheme starts to develop artifacts near the velocity contrast (Figure 5f). The FD method is no longer stable and therefore is not plotted. At
is used, the one-step scheme is stable (Figure 5e) whereas the two-step scheme starts to develop artifacts near the velocity contrast (Figure 5f). The FD method is no longer stable and therefore is not plotted. At ![]() , which corresponds to the Nyquist sampling rate, the one-step scheme remains stable (Figure 5g), but the two-step scheme becomes unstable and thus is not plotted. Using
, which corresponds to the Nyquist sampling rate, the one-step scheme remains stable (Figure 5g), but the two-step scheme becomes unstable and thus is not plotted. Using ![]() , the one-step scheme is still stable, but starts to develop ringing artifacts similar to those observed by Du et al. (2014) (Figure 5h). Using the time step size of
, the one-step scheme is still stable, but starts to develop ringing artifacts similar to those observed by Du et al. (2014) (Figure 5h). Using the time step size of ![]() , the ringing effects aggravate, however the operator remains stable (Figure 5i).
, the ringing effects aggravate, however the operator remains stable (Figure 5i).
|
|
|
|
Lowrank one-step wave extrapolation for reverse-time migration |