Deblending using normal moveout and median filtering in common-midpoint gathers

Median filtering

Conventional median filtering is based on a scalar-value sorting process. When a set of scalars is sorted into an ascending or descending sequence, the middle value is chosen as standard for this sequence. In signal-processing or geophysical data analysis fields, this filter is commonly used to remove spiky noise. The more general mathematical formulation of median filtering is given as:

$$\hat{u}_{i,j}=\arg\min_{u_m\in U_{i,j}}\sum_{l=1}^{L}\Arrowvert u_m-u_l \Arrowvert_p,$$ (5)

where $\hat{u}_{i,j}$ is the output value for location $x_{i,j}$ , $U_{i,j}=\{u_1,u_2,\cdots,u_L\}$ , $i,j$ are the position indices in a 2-D profile, and $l$ and $m$ are both indices in the filtering window. $L$ is the length of the filtering window, and $p$ denotes $L_p$ norm. Commonly $p=1$ corresponds to standard median filtering.

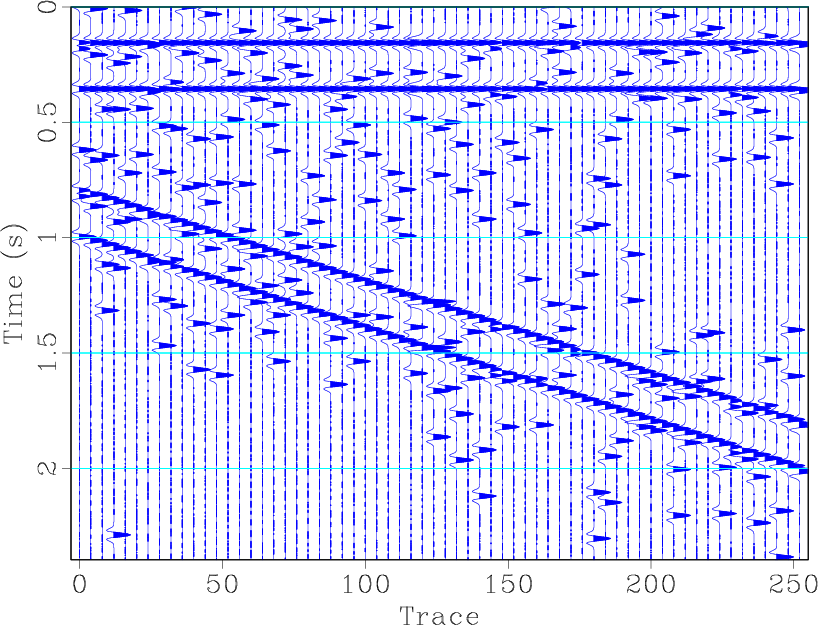
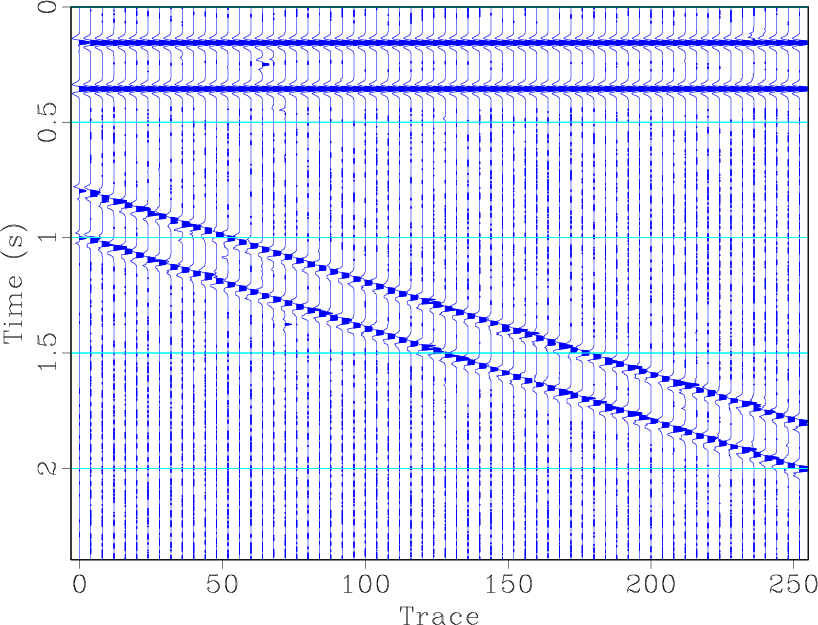
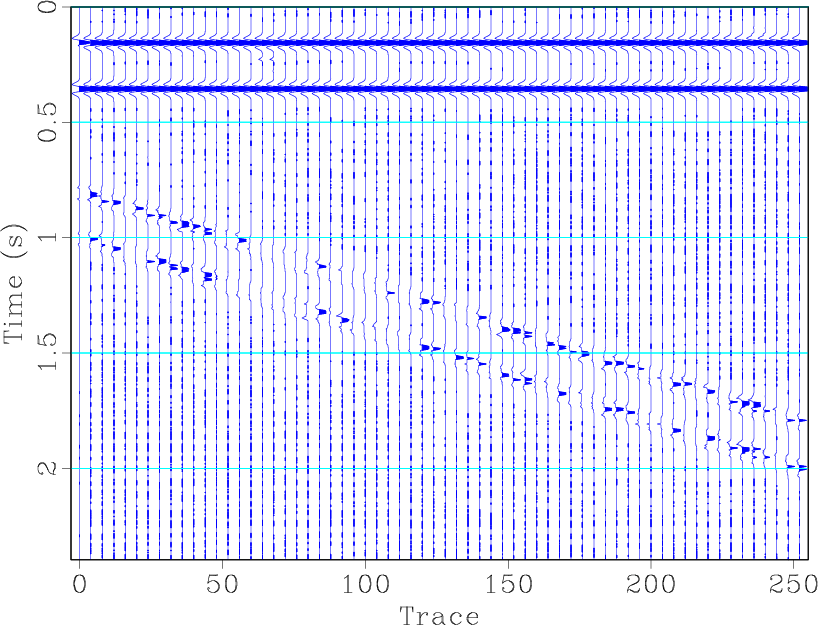
Unlike 2D signalprocessing , where the signal is multi-dimensionally coherent, geophysical data are only spatially coherent. Because of the temporally sparse property, the useful signal turns into a spike-like form. This spatial coherent characteristic requires that conventional median filtering should be taken along the spatial direction. Here, spatial direction means the horizontal direction for a 2D seismic profile. In addition, the local slope of an event should be small in order to preserve more useful energy. Figure 5 shows the effectiveness of median filtering in attenuating blending noise and preserving useful events. Figure 5b corresponds to median filtering along the time direction with a filter length of 11. With this choice, most of the useful energy has been removed. Figure 5c corresponds to median filtering along the spatial direction with a filter length of 7. Figure 5d corresponds to median filtering along the spatial direction with a filter length of 11. When the filter length is set at 7, most of horizontal energy is preserved and some dipping energy is lost. When the filter length is set at 11, most of the dipping energy is lost. Thus, we conclude that using median filtering in a profile with dipping events is dangerous; if the filter length is not appropriately chosen, the energy loss is heavy.

For dipping events, multidimensional median filtering can be used as a substitute (Huo et al., 2012). Multidimensional median filtering, however, requires a precise estimation of the local slope of the seismic events, which may be difficult in field-data processing in the presence of intense random or spiky noise. Besides, using multidimensional median filtering needs much more computational cost and memory. Here, we propose using median filtering after NMO in the CMG, where the events are flatten and the effectiveness of median filtering is maximized.

huos,huos-tmf,huos-xmf7,huos-xmf11
Figure 5. (a) Blended data. (b) Median filtering along the time direction (filter length is 11). (c) Median filtering along space direction (filter length is 7). (d) Median filtering along space direction (filter length is 11).

Deblending using normal moveout and median filtering in common-midpoint gathers