 |
 |
 |
 | Seismic data decomposition into spectral components using regularized nonstationary autoregression |  |
![[pdf]](icons/pdf.png) |
Next: Benchmark tests
Up: Fomel: Regularized nonstationary autoregression
Previous: Regularized nonstationary regression
Prony's method of data analysis was developed originally for
representing a noiseless signal as a sum of exponential components
(Prony, 1795). It was extended later to noisy signals, complex
exponentials, and spectral analysis
(Pisarenko, 1973; Beylkin and Monzón, 2005; Marple, 1987; Bath, 1995). The basic idea follows
from the fundamental property of exponential functions:
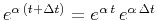 . In
signal-processing terms, it implies that a time sequence
. In
signal-processing terms, it implies that a time sequence
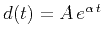 (with real or complex
(with real or complex  ) is predictable
by a two-point prediction-error filter
) is predictable
by a two-point prediction-error filter
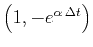 , or, in the Z-transform notation,
, or, in the Z-transform notation,
 |
(6) |
where
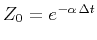 . If the signal is composed of multiple exponentials,
. If the signal is composed of multiple exponentials,
 |
(7) |
they can be predicted simultaneously by using a convolution of several
two-point prediction-error filters:
where
 .
This observation suggests the following three-step algorithm:
.
This observation suggests the following three-step algorithm:
- Estimate a prediction-error filter from the data by determining filter coefficients
 from the least-squares minimization of
from the least-squares minimization of
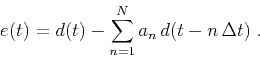 |
(9) |
- Writing the filter as a
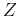 polynomial (equation 8), find its complex roots
polynomial (equation 8), find its complex roots
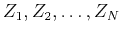 . The exponential factors
. The exponential factors
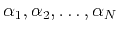 are determined then as
are determined then as
 |
(10) |
- Estimate amplitudes
 of different components in equation 7 by linear least-squares fitting.
of different components in equation 7 by linear least-squares fitting.
Prony's method can be applied in sliding windows, which was a
technique developed by Russian
geophysicists (Mitrofanov and Priimenko, 2011; Gritsenko et al., 2001) for identifying low-frequency
seismic anomalies (Mitrofanov et al., 1998). I propose to extend it to
smoothly nonstationary analysis by applying the following modifications:
- Using RNAR, the filter coefficients
 become smoothly-varying functions of time
become smoothly-varying functions of time  , which allows the filter to adapt to nonstationary changes in the input data.
, which allows the filter to adapt to nonstationary changes in the input data.
- At each instance of time, roots of the corresponding
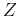 polynomial also become functions of time
polynomial also become functions of time  . I apply a robust, eigenvalue-based algorithm for root finding (Toh and Trefethen, 1994).
The instantaneous frequency of different components
. I apply a robust, eigenvalue-based algorithm for root finding (Toh and Trefethen, 1994).
The instantaneous frequency of different components  is
determined directly from the phase of different roots:
is
determined directly from the phase of different roots:
![\begin{displaymath}
f_n(t) = -Re\left[\arg\left(\frac{\hat{Z}_n(t)}{2\pi\,\Delta t}\right)\right]\;.
\end{displaymath}](img41.png) |
(11) |
- Finally, using RNR, I estimate smoothly-varying amplitudes of different components
 .
.
The nonstationary decomposition model for a complex signal  is thus
is thus
 |
(12) |
and the local phase  corresponds to time integration of the
instantaneous frequency determined in Step 2:
corresponds to time integration of the
instantaneous frequency determined in Step 2:
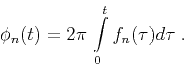 |
(13) |
For ease of analysis, real signals can be transformed to the
complex domain by using analytical traces (Taner et al., 1979).
Subsections
 |
 |
 |
 | Seismic data decomposition into spectral components using regularized nonstationary autoregression |  |
![[pdf]](icons/pdf.png) |
Next: Benchmark tests
Up: Fomel: Regularized nonstationary autoregression
Previous: Regularized nonstationary regression
2013-10-09
![]() . In
signal-processing terms, it implies that a time sequence
. In
signal-processing terms, it implies that a time sequence
![]() (with real or complex
(with real or complex ![]() ) is predictable
by a two-point prediction-error filter
) is predictable
by a two-point prediction-error filter
![]() , or, in the Z-transform notation,
, or, in the Z-transform notation,