Theory

In prestack seismic reflection imaging, a reflector is imaged when the source wavefield coincides with the receiver wavefield in both space and time (Claerbout, 1985). For poststack or zero-offset data, reflectors can be imaged using the exploding reflector concept (Loewenthal et al., 1976). The imaging condition of exploding reflector is similar to that of time-reversal imaging, which states that the backward-propagated wavefield at zero time corresponds to the reflectors/sources. The principle of time-reversal imaging can be used for locating passive earthquake hypocenters (Gajewski and Tessmer, 2005). All the aforementioned imaging conditions require the start times of seismic sources to be available, which is not the case for microseismic data. Therefore, most existing time-reversal imaging algorithms need to perform scanning and picking on a group of potential start times (Maxwell, 2014; Fink, 2006).

Motivated by the development of distributed sensor networks, we propose to adopt the imaging principle of prestack migration for locating microseismic hypocenters. We treat the wavefield back propagated from each individual receiver as an independent wavefield, and define microseismic hypocenters as the locations where all the wavefields coincide in both space and time. The imaging condition is formulated as a multiplication reduction of all the back propagated wavefields, calculated using data from each receiver:

  $$I(\mathbf{x},t) = \prod\limits_{i=0}^{N-1} R_i(\mathbf{x},t) \; .$$ (1)

A similar technique was developed by Nakata (2015, personal communication). Assuming the velocity model is accurate and data contains zero noise, the image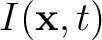 $I(\mathbf{x},t)$ should have non-zero values only if all the backward-propagated wavefields are non-zero at location $\mathbf{x}$ and time $t$, i.e., the starting of an earthquake. When noise is present in the data, extra non-zero values might appear in the image. However, as long as the noise has certain randomness, the amplitude of these false image points will be much weaker than those generated by coherent signal, and thresholding can effectively separate the non-zero values result from noise. 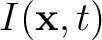The image $I(\mathbf{x},t)$ calculated by equation 1 therefore indicates the seismicity at time $t$. The resolution of the image depends on the frequency content of the wavefields.

The conventional time-reversal imaging can be formulated in a similar fashion. Instead of performing multiplication, the image is produced by summing over all the receiver wavefields:

  $$I(\mathbf{x},t) = \sum\limits_{i=0}^{N-1} R_i(\mathbf{x},t) \; .$$ (2)

In practice, this is done by backward-propagating all the data at once and the summation is implicit. When applied to microseismic data from multiple sources, it is usually a challenging task to pick the hypocenters from the complicated wavefield, especially when the data has a low SNR.

The cross-correlation imaging condition (equation 1) and time-reversal imaging condition (equation 2) represent two extremes. The image produced by equation 1 is high-resolution and easy to pick, since only non-zero values in the image correspond to hypocenters. However, it requires propagating the wavefields using data from each receiver separately, and thus is computationally intensive. Equation 2, on the other hand, requires essentially only one computation using the entire data set, but has less resolving power and is less suitable for distributed networks. A hybrid imaging condition would combine the merits of the two:

  $$I(\mathbf{x},t) = \prod\limits_{j=0}^{N/n-1} \sum\limits_{k=0}^{n-1} R_{j \times n+k}(\mathbf{x},t) \; ,$$ (3)

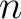where $n$ is the local summation window length. Length 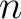$n$ should be selected such that neighboring receivers are backward-propagated together while far-apart receivers are cross-correlated. Equation 3 requires 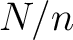$N/n$ computations of reverse-time modeling. In principle, both equation 1 and 3 need to perform cross-correlation using at least three wavefields to constrain one point in space. Schematically, the differences between the three imaging conditions is shown in Figure 1.

ic
Figure 1. Different imaging conditions for locating microseismic sources. A homogeneous medium and four receiver stations are assumed. A hybrid imaging condition calculates local summation before applying cross-correlation. In practice, the summation is performed implicitly by back propagating data from several neighboring receivers at once.

A movie of accumulated seismicity can be generated by performing an integration over time:

  $$M(\mathbf{x},t) = \int \limits_0^t I(\mathbf{x},\tau) d\tau \; ,$$ (4)

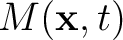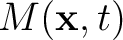Movie $M(\mathbf{x},t)$ is an evolving map of microseismicity in time that could be used to indicate rupture propagation. An image of all the sources corresponds the last instance of $M(\mathbf{x},t)$.