Matching and merging high-resolution and legacy seismic images

P-cable Example

Our second example refers to data from the inner shelf of the Gulf of Mexico, just off of San Luis Pass, Texas (Meckel et al., 2017). The high-resolution P-cable data set was acquired from a shallow marine environment in the Gulf of Mexico. The area of interest for this survey was the near subsurface, and a high frequency source was used which allows for exceptional resolution in the shallow section, at the expense of less coherent signal information at depth caused by attenuation (Meckel and Mulcahy, 2016). In addition, very little low-frequency information is present in the P-cable data because of the high-frequency source used, which makes balancing spectral content particularly difficult. The other image comes from legacy data coverage over the same area, which has better signal continuity at depth than the high-resolution P-cable data. This is apparent by looking at the first few hundred milliseconds of data for both data sets (Figure 8).

window1,window2
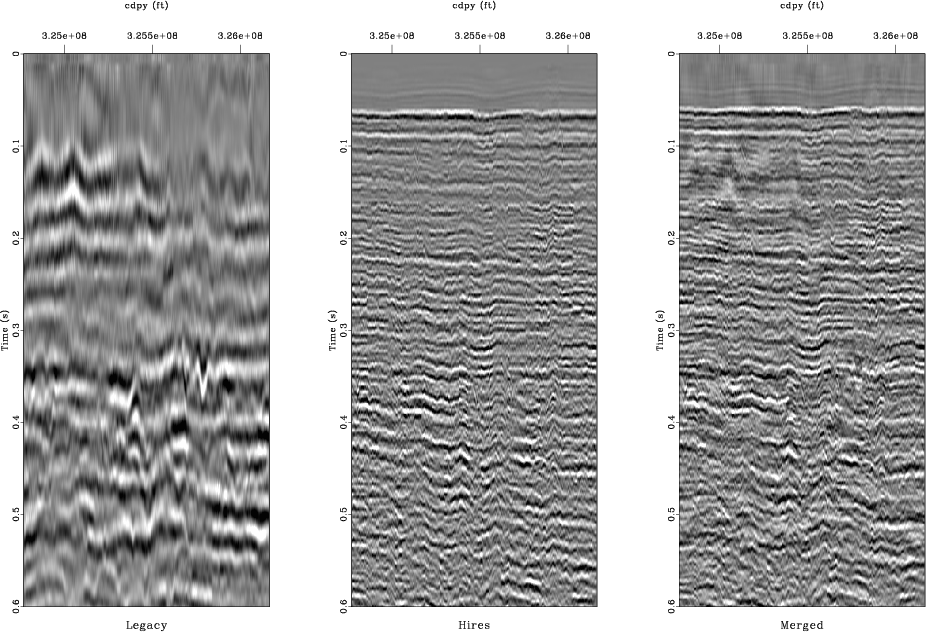
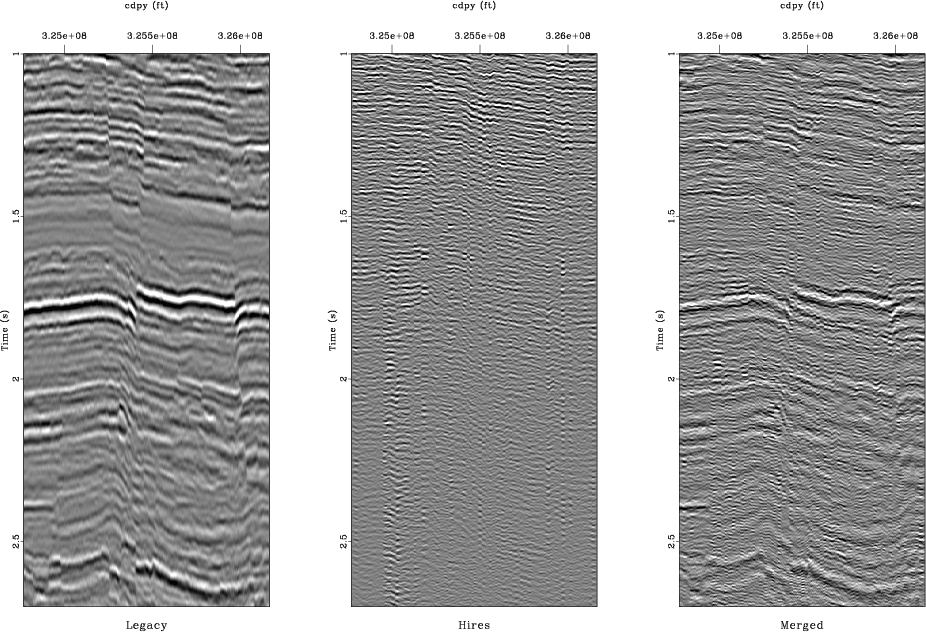
Figure 8. The first 600 ms of data from a sample line from the legacy, high-resolution, and merged image (a). The same images with depth for the legacy, high-resolution, and merged images (b). The merged image resembles the high-resolution image in the shallow parts and incorporates the more coherent lower frequency information from the legacy image with depth.

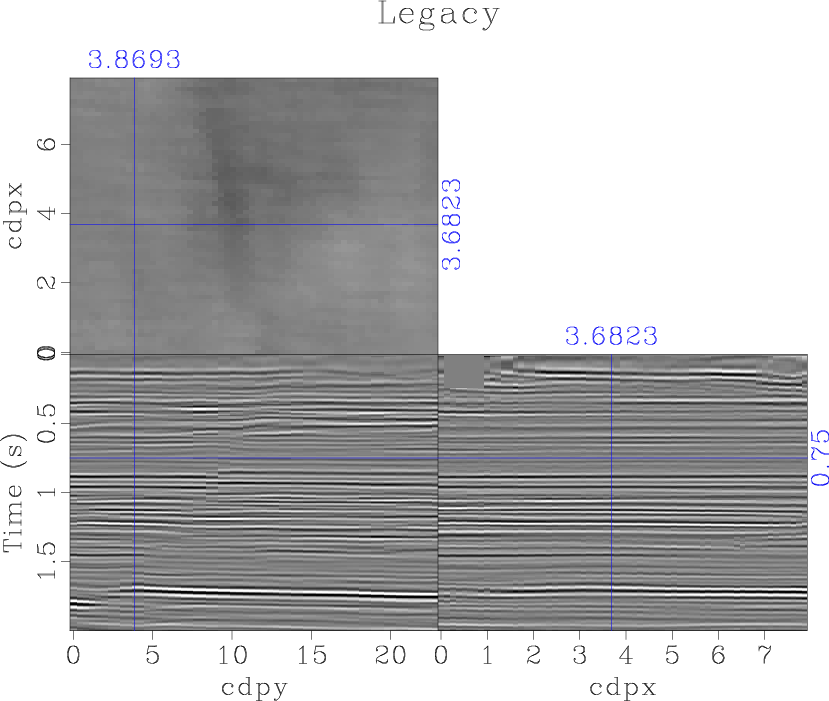
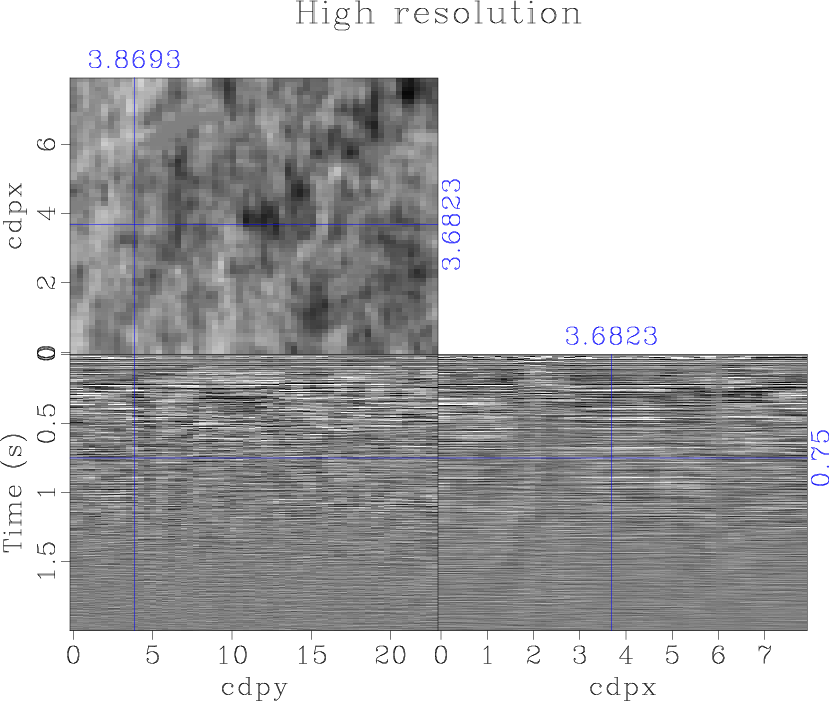
Due to the nature of acquisition, the high resolution image has very dense spatial coverage, providing detailed time slices of the near subsurface (Meckel and Mulcahy, 2016). The legacy image has lower spatial resolution. As a result, when matching the high-resolution and legacy images spatially, the high spatial resolution of the high-resolution image must be degraded to match that of the legacy image. We rebinned the legacy and high-resolution images to align them spatially for comparison (Figure 10). We chose to spatially down-sample the high-resolution image to match the legacy image as opposed to interpolating the legacy image to the high-resolution image's spatial grid to prevent potentially introducing inaccurate data in the merged image.

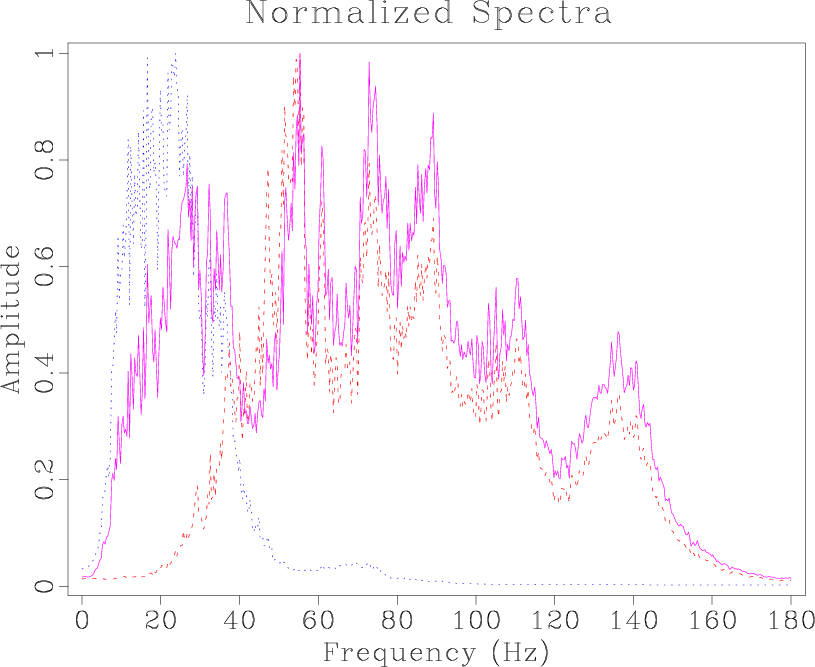
There is a definite separation in frequency content when comparing the legacy and high-resolution images (Figure 9). Because there is not much overlap in frequency bandwidth, balancing their spectral content is challenging. In addition, a primary assumption made in deriving the theoretical smoothing radius (equation 6) is that the signal is modeled by a summation of Ricker wavelets, which may not be a correct assumption. As a result, additional steps must be taken beyond applying the smoothing specified by equation (6) to ensure matching frequency content.

We first apply a low-cut filter to the legacy data to remove the low frequency information that is simply not present in the high-resolution image. Next, we adjust the non-stationary smoothing radius using a simple iterative algorithm (Greer and Fomel, 2017).

The main premise behind the algorithm comes from the fact that, in general, the greater the smoothing radius at a specified point, the more high frequencies are attenuated by smoothing. We choose an initial guess of the non-stationary smoothing radius before applying corrections based on two primary assumptions:

1. The smoothing radius is too small at a specified point if, after smoothing, the high-resolution image has higher local frequency than the legacy image. Thus, the smoothing radius must be increased at that point.
2. The smoothing radius is too large at a specified point if, after smoothing, the high-resolution image has lower local frequency than the legacy image. Thus, the smoothing radius must be decreased at that point.

We apply these assumptions using a line-search method:

$$\mathbf{R}^{(i+1)} = \mathbf{R}^{(i)}+ \alpha \mathbf{r}^{(i)},$$ (10)

where $\mathbf{R}^{(i)}$ is the smoothing radius at the $i$th iteration, $\alpha$ is a scalar constant that can be thought of as the step length, and $\mathbf{r}^{(i)}$ is the residual at the $i$th iteration, which can be thought of as the search direction, and is defined as

$$\mathbf{r} = \mathbf{F}[\mathbf{S}_{\mathbf{R}} \mathbf{d}_h] - \mathbf{F}[\mathbf{d}_l]\;,$$ (11)

where $\mathbf{S}_\mathbf{R}$ is the non-stationary smoothing operator of smoothing radius $\mathbf{R}$, $\mathbf{d}_h$ is the high-resolution image, $\mathbf{d}_l$ is the legacy image, and $\mathbf{F}$ is the local frequency operator. It can be noted that when equation (11) is positive, the high-resolution image still has a higher local frequency value at that specific point than the legacy image, thus the high-resolution image is under-smoothed and the smoothing radius should be increased at that point. This follows the form of the first assumption. The second assumption is used when equation (11) is negative. When equation (11) is zero, the correct radius has been found and no further corrections are made. Thus, it is justifiable to set the search direction from equation (7) equal to the residual.

Using this method, we can continually adjust the smoothing radius until we achieve the desired result of balancing the local frequency content between the two images. In practice, this method produces an acceptable solution in approximately 5 iterations and exhibits sublinear convergence. We smooth the high-resolution image with the radius this method produces to balance local frequency content between the two images.

After this, we use the low-cut filtered legacy and smoothed high-resolution images to find estimated time shifts we need to apply to the high-resolution image to align the reflections with the legacy image. Then, we apply this estimated time shift to the original high-resolution image and blend it with the original legacy image as specified by equations (7) and (9).

The resultant merged image is shown in Figure 10c. The frequency content of the merged image is shown in Figure 9. Here, the merged image spans the frequency bandwidth of the two initial images, thus producing a high resolution volume including optimal signal characteristics from the two initial images.

nspectra2
Figure 9. The spectral content of the entire image display of the legacy (red dashed), high-resolution (blue dotted), and resultant merged (magenta solid) images for the second data set.

legacy4,hires4,merge3
Figure 10. The legacy (a), high-resolution (b), and resultant merged (c) images of the second data set.

Matching and merging high-resolution and legacy seismic images