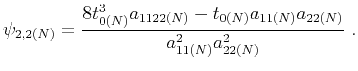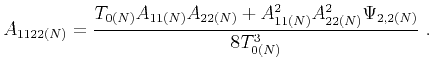|
 |
 |
 | Theory of interval traveltime parameter estimation in layered anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Comparison with known expressions
Up: Coefficients of traveltime expansion
Previous: Formulas for interval NMO
Similarly to the derivation for 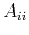 , we have first,
, we have first,
 |
(50) |
which can be calculated for interval
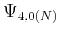 in the
in the  -th layer using,
-th layer using,
 |
(51) |
Subsequently, interval
 in the
in the  -th layer can be computed from,
-th layer can be computed from,
 |
(52) |
where
 . Equation 52 is similar to the Dix-type formula proposed by Tsvankin and Thomsen (1994) for the VTI case. Similar expressions can be derived for
. Equation 52 is similar to the Dix-type formula proposed by Tsvankin and Thomsen (1994) for the VTI case. Similar expressions can be derived for  by considering
by considering
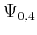 and
and 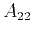 instead of
instead of
 and
and  . To derive the corresponding expression for
. To derive the corresponding expression for  , we follow an analogous procedure ,which leads to
, we follow an analogous procedure ,which leads to
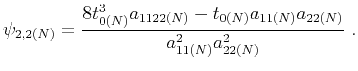 |
(53) |
Using
 |
(54) |
 in the
in the  -th layer can be computed as
-th layer can be computed as
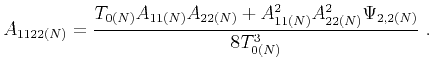 |
(55) |
 |
 |
 |
 | Theory of interval traveltime parameter estimation in layered anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Comparison with known expressions
Up: Coefficients of traveltime expansion
Previous: Formulas for interval NMO
2017-04-14
![]() , we have first,
, we have first,