 |
 |
 |
 | Theory of interval traveltime parameter estimation in layered anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: General formulas for traveltime
Up: Sripanich & Fomel: Interval
Previous: Introduction
Assuming the Einstein repeated-indices summation convention, we can expand the one-way traveltime  into a Taylor series of half offset
into a Taylor series of half offset  (
( or 2 in 3D) around zero offset as follows:
or 2 in 3D) around zero offset as follows:
 |
(1) |
where 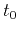 is one-way vertical traveltime,
is one-way vertical traveltime,
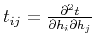 and
and
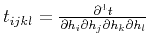 are second- and fourth-order derivative tensors, respectively. Both tensors are symmetric thanks to the symmetry of mixed derivatives. Analogously, we can also derive, for the negative half offset
are second- and fourth-order derivative tensors, respectively. Both tensors are symmetric thanks to the symmetry of mixed derivatives. Analogously, we can also derive, for the negative half offset  ,
,
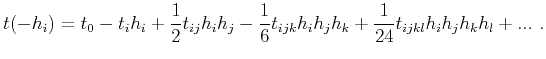 |
(2) |
Assuming pure-mode reflections with source-receiver reciprocity, we can sum the two expansions (equations 1 and 2) for the two legs of rays to derive the expansion of the two-way traveltime as follows (Al-Dajani and Tsvankin, 1998):
 |
(3) |
Equation 3 can be additionally transformed into the series of the squared two-way traveltime in terms of the full offset
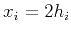 as follows:
as follows:
 |
(4) |
where
In consideration of the symmetry of the time derivative tensors, the quadratic and quartic terms in equation 4 reduce to the following known expressions (Al-Dajani et al., 1998):
In the derivation of the general formulas for moveout coefficients in the next section, we keep the tensor notation, which simplifies the use of tensor operations. We also use the fact that, in the case of horizontally stacked layers, the half-offset  and reflection traveltime
and reflection traveltime 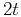 can be expressed in terms of horizontal slownesses (ray parameters)
can be expressed in terms of horizontal slownesses (ray parameters)  and
and  in
in  and
and  directions as follows:
directions as follows:
where  and
and
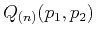 denote the thickness and the vertical slowness of the
denote the thickness and the vertical slowness of the  -th layer. The derivation of equations 9 and 10 is included in the appendix. The general dependence
-th layer. The derivation of equations 9 and 10 is included in the appendix. The general dependence
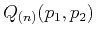 follows directly from the Christoffel equation. Throughout the text, we use the subscript index in parentheses to indicate the corresponding layer. The upper-case and lower-case letters denote interval and effective parameters respectively.
follows directly from the Christoffel equation. Throughout the text, we use the subscript index in parentheses to indicate the corresponding layer. The upper-case and lower-case letters denote interval and effective parameters respectively.
 |
 |
 |
 | Theory of interval traveltime parameter estimation in layered anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: General formulas for traveltime
Up: Sripanich & Fomel: Interval
Previous: Introduction
2017-04-14
![]() and reflection traveltime
and reflection traveltime ![]() can be expressed in terms of horizontal slownesses (ray parameters)
can be expressed in terms of horizontal slownesses (ray parameters) ![]() and
and ![]() in
in ![]() and
and ![]() directions as follows:
directions as follows: