 |
 |
 |
 | Theory of interval traveltime parameter estimation in layered anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Comparison with the method
Up: Comparison with known expressions
Previous: Comparison with known expressions
Al-Dajani et al. (1998) suggest to compute the effective quartic term using the VTI formula given by equation 62. The independent parameters in each layer are substituted by their azimuthally variant counterparts as follows:
where 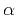 denotes the azimuth angle measured from [
denotes the azimuth angle measured from [ ,
, ] plane,
] plane, 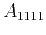 ,
,  , and
, and  are given in equations 58-60. The effective
are given in equations 58-60. The effective 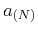 computed based on equation 62 is then multiplied by the source-receiver distance along the CMP line (offset in polar coordinates) and summed with lower-order terms for traveltime computation in polar coordinates. The relative error in the quartic term computation is shown in Figure 1a.
computed based on equation 62 is then multiplied by the source-receiver distance along the CMP line (offset in polar coordinates) and summed with lower-order terms for traveltime computation in polar coordinates. The relative error in the quartic term computation is shown in Figure 1a.
 |
 |
 |
 | Theory of interval traveltime parameter estimation in layered anisotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Comparison with the method
Up: Comparison with known expressions
Previous: Comparison with known expressions
2017-04-14