 |
 |
 |
 | On anelliptic approximations for  velocities in
transversally isotropic media
velocities in
transversally isotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Muir approximation
Up: On anelliptic approximations for
Previous: Introduction
Wavefront propagation in the general anisotropic media can be
described with the anisotropic eikonal equation
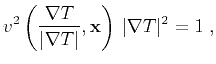 |
(1) |
where
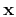 is a point in space,
is a point in space,
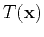 is the
traveltime at that point for a given source, and
is the
traveltime at that point for a given source, and
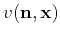 is the phase velocity in the phase direction
is the phase velocity in the phase direction
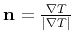 .
.
In the case of VTI media, the three modes of elastic wave propagation
(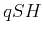 ,
, 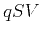 , and
, and  ) have the following well-known explicit
expressions for the phase velocities (Gassmann, 1964):
) have the following well-known explicit
expressions for the phase velocities (Gassmann, 1964):
where, in the notation of Backus (1962) and Berryman (1979),
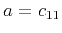 ,
, 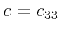 ,
, 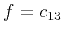 ,
, 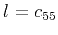 ,
, 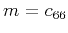 ,
,
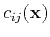 are the density-normalized components of the elastic tensor, and
are the density-normalized components of the elastic tensor, and 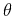 is
the phase angle between the phase direction
is
the phase angle between the phase direction
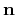 and the axis of
symmetry.
and the axis of
symmetry.
The group velocity describes the propagation of individual ray trajectories
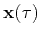 . It can be determined from the phase velocity using the
general expression
. It can be determined from the phase velocity using the
general expression
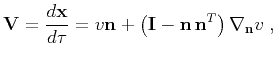 |
(5) |
where
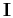 denotes the identity matrix,
denotes the identity matrix,
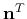 stands for the
transpose of
stands for the
transpose of
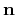 , and
, and
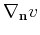 is the gradient
of
is the gradient
of 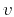 with respect to
with respect to
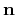 . The two terms in
equation (5) are clearly orthogonal to each other. Therefore, the
group velocity magnitude is
(Berryman, 1979; Byun, 1984; Postma, 1955)
. The two terms in
equation (5) are clearly orthogonal to each other. Therefore, the
group velocity magnitude is
(Berryman, 1979; Byun, 1984; Postma, 1955)
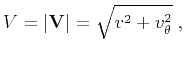 |
(6) |
where
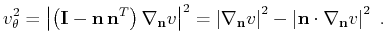 |
(7) |
The group velocity has a particularly simple form in the case of elliptic
anisotropy. Specifically, the phase velocity squared has the
quadratic form
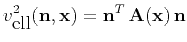 |
(8) |
with a symmetric positive-definite matrix
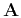 , and the group
velocity is
, and the group
velocity is
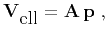 |
(9) |
where
 .
The corresponding group slowness squared has the explicit expression
.
The corresponding group slowness squared has the explicit expression
 |
(10) |
where
 is the group direction, and
is the group direction, and
 is the matrix
inverse of
is the matrix
inverse of
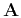 . For example, the elliptic expression (2) for
the phase velocity of
. For example, the elliptic expression (2) for
the phase velocity of 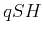 waves in VTI media transforms into a completely
analogous expression for the group slowness
waves in VTI media transforms into a completely
analogous expression for the group slowness
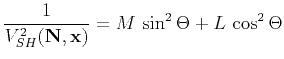 |
(11) |
where 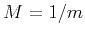 ,
, 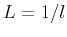 , and
, and 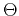 is the angle between the group direction
is the angle between the group direction
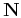 and the axis of symmetry.
and the axis of symmetry.
The situation is more complicated in the anelliptic case.
Figure 1 shows the  and
and 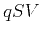 phase velocity profiles in a
transversely isotropic material - Greenhorn shale (Jones and Wang, 1981),
which has the parameters
phase velocity profiles in a
transversely isotropic material - Greenhorn shale (Jones and Wang, 1981),
which has the parameters
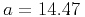 km
km s
s ,
,
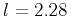 km
km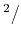 s
s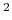 ,
,
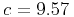 km
km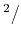 s
s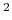 , and
, and
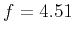 km
km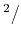 s
s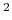 . Figure 2 shows the
corresponding group velocity profiles. The non-convexity of the
. Figure 2 shows the
corresponding group velocity profiles. The non-convexity of the 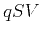 phase
velocity causes a multi-valued (triplicated) group velocity profile. The
shapes of all the surfaces are clearly anelliptic.
phase
velocity causes a multi-valued (triplicated) group velocity profile. The
shapes of all the surfaces are clearly anelliptic.
|
|---|
exph
Figure 1. Phase velocity profiles for  (outer curve) and
(outer curve) and
 (inner curve) waves in a transversely isotropic material (Greenhorn
shale).
(inner curve) waves in a transversely isotropic material (Greenhorn
shale).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[sage]](icons/sage.png)
|
|---|
|
|---|
exgr
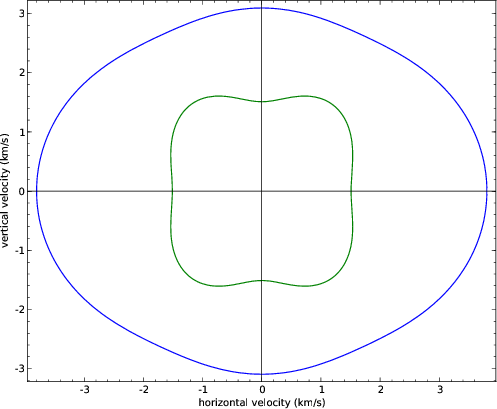
Figure 2. Group velocity profiles for  (outer curve) and
(outer curve) and
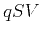 (inner curve) waves in a transversely isotropic material (Greenhorn
shale).
(inner curve) waves in a transversely isotropic material (Greenhorn
shale).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[sage]](icons/sage.png)
|
|---|
A simple model of anellipticity is suggested by the Muir approximation
(Dellinger et al., 1993; Muir and Dellinger, 1985), reviewed in the next section.
 |
 |
 |
 | On anelliptic approximations for  velocities in
transversally isotropic media
velocities in
transversally isotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Muir approximation
Up: On anelliptic approximations for
Previous: Introduction
2014-05-14
![]() ,
, ![]() , and
, and ![]() ) have the following well-known explicit
expressions for the phase velocities (Gassmann, 1964):
) have the following well-known explicit
expressions for the phase velocities (Gassmann, 1964):
![]() . It can be determined from the phase velocity using the
general expression
. It can be determined from the phase velocity using the
general expression
![]() and
and ![]() phase velocity profiles in a
transversely isotropic material - Greenhorn shale (Jones and Wang, 1981),
which has the parameters
phase velocity profiles in a
transversely isotropic material - Greenhorn shale (Jones and Wang, 1981),
which has the parameters
![]() km
km![]() s
s![]() ,
,
![]() km
km![]() s
s![]() ,
,
![]() km
km![]() s
s![]() , and
, and
![]() km
km![]() s
s![]() . Figure 2 shows the
corresponding group velocity profiles. The non-convexity of the
. Figure 2 shows the
corresponding group velocity profiles. The non-convexity of the ![]() phase
velocity causes a multi-valued (triplicated) group velocity profile. The
shapes of all the surfaces are clearly anelliptic.
phase
velocity causes a multi-valued (triplicated) group velocity profile. The
shapes of all the surfaces are clearly anelliptic.

