|
|
|
|
Accelerated plane-wave destruction |
Gauss-Newton's iteration searches the solutions for nonlinear equation
6 as follows:
Let ![]() be the estimated slope at step
be the estimated slope at step ![]() ,
with estimating error (or destructive error)
,
with estimating error (or destructive error)
![]() .
In order to find the correct solution
.
In order to find the correct solution ![]() that minimizes
that minimizes ![]() ,
we need to find the increment
,
we need to find the increment ![]() from the local linearization:
from the local linearization:
The iterative algorithm stops when a stationary point
or a root of ![]() is reached. They are:
is reached. They are:
The iterative algorithm for equation 6
may converge at different points,
depending on the initial point that we chose;
![]() is a common practical choice for the initial solution.
In this case,
the iterative algorithm may converge to the least absolute root,
which denotes the event with smallest dip angle.
is a common practical choice for the initial solution.
In this case,
the iterative algorithm may converge to the least absolute root,
which denotes the event with smallest dip angle.
In order to analyze the convergence results,
the maximally flat fractional delay filter
(Thiran, 1971; Zhang, 2009)
is designed with polynomial coefficients:
Since ![]() is a polynomial of
is a polynomial of ![]() ,
expanding it, we get
,
expanding it, we get
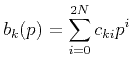 and
and
 |
(9) |
| (10) |
Substituting the above two equations,
the nonlinear equation 6
becomes a ![]() -th degree polynomial equation for
-th degree polynomial equation for ![]() :
:
![\begin{displaymath}
a_i=[1-(-1)^iZ_x]\sum_{k=-N}^Nc_{ki}Z_t^{-k}U,
\end{displaymath}](img69.png) |
(12) |
 and the spatial filter
and the spatial filter
In the special case of ![]() ,
we get a three-point approximation of
,
we get a three-point approximation of ![]() .
It takes the following form (Fomel, 2002):
.
It takes the following form (Fomel, 2002):
| (13) |
| (14) |
In this case,
the quadratic plane-wave destruction equation 11
has one stationary point and two roots,
which can be analytically expressed as:
![]() , where
, where
![]() .
.
The plots in Figure 1 show the convergence process
of the iterative algorithm when we choose ![]() as the starting value.
Geometrically when
as the starting value.
Geometrically when ![]() ,
the iteration converges to the stationary point
,
the iteration converges to the stationary point
![]() ,
as shown in Figure 1a.
When
,
as shown in Figure 1a.
When ![]() ,
it converges to the least absolute solution of equation 11.
Figure 1b and 1c
shows the convergence process
to the least absolute solution in different cases.
We can summarize the convergence result of the iterative algorithm as follows:
,
it converges to the least absolute solution of equation 11.
Figure 1b and 1c
shows the convergence process
to the least absolute solution in different cases.
We can summarize the convergence result of the iterative algorithm as follows:
As
 in the above equation, we use
in the above equation, we use
 instead of
instead of
 to obtain better numerical stability.
to obtain better numerical stability.
When the data is polluted by noise,
in order to obtain a robust slope estimation,
we can combine the equations in a local window into the following equation set:
| (19) |
| (20) |
In 3D applications, there are two polynomial PWD equations
for inline and crossline slopes separately.
Note that, using the decoupling,
inline and crossline slope estimations can share
the temporal filtering results in equations 15![]() 17.
We can obtain the coefficients of the crossline
plane-wave destruction equation as
17.
We can obtain the coefficients of the crossline
plane-wave destruction equation as
| (21) |
The five-point or longer approximations of ![]() can achieve higher accuracy.
Equation 6 in this case becomes
a higher-order polynomial equation (see details in the Appendix),
which can be solved numerically.
However, there are multiple stationary points,
and it is difficult to determine the right one analytically.
For applications that need five-point or higher accuracy,
we suggest obtaining an initial slope estimation by
the proposed three-point method and
using it to make the iterative algorithm converge faster
(to decrease
can achieve higher accuracy.
Equation 6 in this case becomes
a higher-order polynomial equation (see details in the Appendix),
which can be solved numerically.
However, there are multiple stationary points,
and it is difficult to determine the right one analytically.
For applications that need five-point or higher accuracy,
we suggest obtaining an initial slope estimation by
the proposed three-point method and
using it to make the iterative algorithm converge faster
(to decrease ![]() ).
).
|
|
|
|
Accelerated plane-wave destruction |