Estimating local frequency by complex non-stationary autoregression

Next: Preparing smoothly variable frequency Up: Method Previous: 1D non-stationary seislet transform

Estimating local frequency by complex non-stationary autoregression

According to the autoregressive spectral analysis theory (Marple, 1987), a complex time series that has a constant frequency component is predictable by a two-point prediction-error filter $(1,-e^{i\omega_0\Delta t})$ . Suppose a complex time series is

. In Z-transform notation, the two-point prediction-error filter can be expressed as:

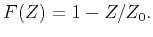$\displaystyle F(Z)=1-Z/Z_0.$

(13)

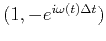We assume that a 1D time series has a smooth frequency component, then the 1D time series can be locally predicted using different local two-point prediction-error filters $(1,-e^{i\omega(t)\Delta t})$ :

$\displaystyle d(t)=e^{i\omega(t)\Delta t}d(t-\Delta t).$

(14)

In order to estimate $\omega(t)$ using equation 14, we need to first minimize the least-squares misfit of the true and predicted time series with a local-smoothness constraint:

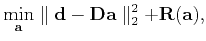$\displaystyle \min_{\mathbf{a}} \parallel \mathbf{d} - \mathbf{D} \mathbf{a} \parallel_2^2 + \mathbf{R}(\mathbf{a}),$

(15)

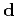where $\mathbf{d}$ and $\mathbf{a}$ are vectors composed of the entries

and

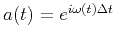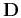, respectively, and $a(t)=e^{i\omega(t)\Delta t}$ . $\mathbf{D}$ is a diagonal matrix composed of the entries 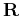$d(t-\Delta t)$ . $\mathbf{R}$ denotes the local-smoothness constraint. Equation 15 can be solved using shaping regularization:

$\displaystyle \hat{\mathbf{a}} = [\lambda^2\mathbf{I}+\mathcal{T}(\mathbf{D}^T\mathbf{D}-\lambda^2\mathbf{I})]^{-1}\mathcal{T}\mathbf{D}^T\mathbf{d},$

(16)

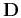where $\mathcal{T}$ is a triangle smoothing operator and $\lambda$ is a scaling parameter that controls the physical dimensionality and enables fast convergence. $\lambda$ can be chosen as the least-squares norm of $\mathbf{D}$ . After the filter coefficient

is obtained, we can straightforwardly calculate the local angular frequency $\omega(t)$ by

$\displaystyle \omega(t) = Re\left[\frac{\mbox{arg}(a(t))}{\Delta t}\right].$

(17)

Next: Preparing smoothly variable frequency Up: Method Previous: 1D non-stationary seislet transform

2019-02-12