next up previous Random noise attenuation by $ f$ -$ x$ empirical mode decomposition predictive filtering [pdf]

Next: f-x empirical mode decomposition Up: Empirical mode decomposition Previous: 1D EMD

f-x EMD

Instead of 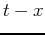$ t-x$ domain EMD, a $ f-x$ domain EMD method to attenuate random noise in seismic data has been proposed by Bekara and van der Baan (2009). They apply EMD on each frequency slice in the $ f-x$ domain, and suppress the higher wavenumber components, which mainly represent random noise. However, a problem occurs when applying $ f-x$ EMD, because the high-wavenumber dipping events will also be removed. This problem occurs because, for many data sets, the random noise and any steeply dipping coherent energy make a significantly larger contribution to the high-wavenumber energy in the f-x domain than any desired signal (Bekara and van der Baan, 2009).

Bekara and van der Baan (2009) cleverly utilize this by-product of $ f-x$ EMD to attenuate coherent noise such as ground roll.

The detailed algorithmic steps of $ f-x$ EMD are given by Bekara and van der Baan (2009) as:

  1. Select a time window and transform the data to the $ f-x$ domain.
  2. For every frequency,
    1. separate real and imaginary parts in the spatial sequence,
    2. compute IMF1, for the real signal and subtract it to obtain the filtered real signal,
    3. repeat for the imaginary part,
    4. combine to create the filtered complex signal.
  3. Transform data back to the 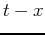$ t-x$ domain.
  4. Repeat for the next time window.

$ f-x$ EMD can be used as an adaptive 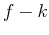$ f-k$ filter. The cutoff wavenumber is adaptively defined and does not need any apriori knowledge about the seismic data in order to define the filter parameters. This adaptability makes $ f-x$ EMD very convenient to utilize in real applications. The frequency-slice-dependent adaptability also makes $ f-x$ EMD more precise than $ f-x$ predictive filtering, because all the filter parameters in $ f-x$ predictive filtering for each frequency slice are the same. Another advantage of $ f-x$ EMD over $ f-x$ predictive filtering is that the trace spacing does not need to be perfectly regular because no convolutional operator is used, a characteristic similar to local median and SVD filtering (Bekara and van der Baan, 2007,2009).

sigimf
sigimf
Figure 2. Demonstration of empirical mode decomposition on a synthetic signal. (a) The original signal, (b) first IMF, (c) second IMF, (d) third IMF, (e) residual.
[pdf] [png] [scons]

next up previous Random noise attenuation by $ f$ -$ x$ empirical mode decomposition predictive filtering [pdf]

Next: f-x empirical mode decomposition Up: Empirical mode decomposition Previous: 1D EMD

2014-08-20