 |
 |
 |
 | Random noise attenuation by  -
- empirical mode decomposition predictive filtering
empirical mode decomposition predictive filtering |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Chen & Ma: EMD
Previous: Bibliography
In this appendix, we review the sifting algorithm of empirical mode decomposition (equation 6 in the main paper).
For the original signal, we first find the local maxima and minima of the signal. Once identified, fit these local maxima and minima by cubic spline interpolation in turn in order to generate the upper and lower envelopes. Then compute the mean of the upper and lower envelopes 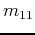 , the difference between the data and first mean
, the difference between the data and first mean 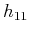 .
.
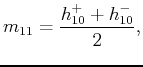 |
(9) |
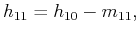 |
(10) |
where 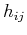 denotes the remaining signal after
denotes the remaining signal after 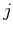 th sifting for generating the
th sifting for generating the 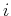 th IMF,
th IMF, 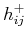 and
and 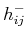 are corresponding upper and lower envelopes, respectively, and
are corresponding upper and lower envelopes, respectively, and 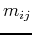 is the mean of upper and lower envelopes after
is the mean of upper and lower envelopes after 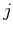 th sifting for generating the
th sifting for generating the 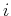 th IMF.
Repeating the sifting procedure (A-2)
th IMF.
Repeating the sifting procedure (A-2) 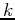 times, until
times, until 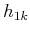 reach the prerequisites of IMF, these are:
reach the prerequisites of IMF, these are:
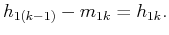 |
(11) |
The criterion for the sifting process to stop is given by Huang et al. (1998) as:
![$\displaystyle 0.2\le SD=\sum_{t=0}^{T}\left[\frac{\vert h_{1(k-1)}(t)-h_{1k}(t)\vert^2}{h^2_{1(k-1)}}\right]\le 0.3,$](img78.png) |
(12) |
where 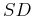 denotes the standard deviation.
When
denotes the standard deviation.
When 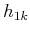 is considered as an IMF, let
is considered as an IMF, let
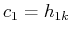 , we separate the first IMF from the original data:
, we separate the first IMF from the original data:
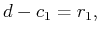 |
(13) |
where 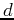 is the original signal,
is the original signal, 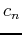 denotes the
denotes the 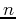 th IMF, and
th IMF, and 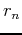 is the residual after the
is the residual after the 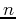 th IMF based sifting.
Repeating the sifting process from equation A-1 to A-5, changing
th IMF based sifting.
Repeating the sifting process from equation A-1 to A-5, changing 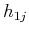 to
to 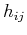 , in order to get the following IMFs:
, in order to get the following IMFs:
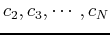 .
The sifting process can be stopped when the residual
.
The sifting process can be stopped when the residual 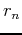 , becomes so small that it is less than a predetermined value of substantial consequence, or when
, becomes so small that it is less than a predetermined value of substantial consequence, or when 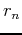 becomes a monotonic function from which no more IMF can be extracted.
becomes a monotonic function from which no more IMF can be extracted.
Finally, we achieved a decomposition of the original data into N modes, and one residual, as shown in equation 6 in the main context.
 |
 |
 |
 | Random noise attenuation by  -
- empirical mode decomposition predictive filtering
empirical mode decomposition predictive filtering |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Chen & Ma: EMD
Previous: Bibliography
2014-08-20
![]() , the difference between the data and first mean
, the difference between the data and first mean ![]() .
.