 |
 |
 |
 | Kirchhoff migration using eikonal-based computation of traveltime source-derivatives |  |
![[pdf]](icons/pdf.png) |
Next: Numerical Implementation
Up: Theory and Implementation
Previous: Theory and Implementation
The point-source traveltime 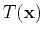 clearly depends on the source location
clearly depends on the source location 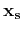 . To
explicitly show such a dependency in the eikonal equation, we define a relative coordinate
. To
explicitly show such a dependency in the eikonal equation, we define a relative coordinate 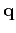 as
as
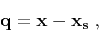 |
(2) |
and use
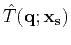 to denote traveltime in the relative coordinates. After
inserting this definition into equation 1, we obtain
to denote traveltime in the relative coordinates. After
inserting this definition into equation 1, we obtain
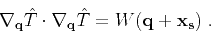 |
(3) |
Here the differentiation
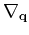 stands for gradient operator in
the relative coordinate
stands for gradient operator in
the relative coordinate 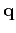 and is taken with a fixed source location
and is taken with a fixed source location 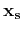 .
In 3D, if
.
In 3D, if
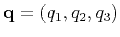 and denoting
and denoting 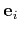 with
with 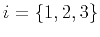 to be
the unit vector in depth, inline and crossline directions, respectively, then
to be
the unit vector in depth, inline and crossline directions, respectively, then
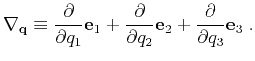 |
|
|
(4) |
Since we are interested in the traveltime derivative with respect to the source, i.e.
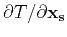 , we take directional derivative
, we take directional derivative
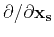 to
to
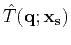 and apply the chain-rule
according to equation 2:
and apply the chain-rule
according to equation 2:
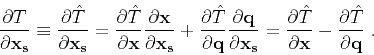 |
(5) |
Equation 5 results in a vector that contains the traveltime source-derivatives in
depth, inline and crossline directions. In accordance with
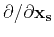 ,
,
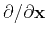 and
and
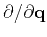 are also directional
derivatives. All numerical examples in this paper are based on a typical 2D acquisition, where we
assume a constant source depth and thus only the inline traveltime source-derivative is of interest.
The quantity
are also directional
derivatives. All numerical examples in this paper are based on a typical 2D acquisition, where we
assume a constant source depth and thus only the inline traveltime source-derivative is of interest.
The quantity
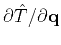 coincides with the slowness vector of the
ray that originates from
coincides with the slowness vector of the
ray that originates from 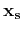 . For a finite-difference eikonal solver such as FMM and
FSM, it is usually estimated by an upwind scheme during traveltime computations at each grid point
and thus can be easily extracted. Applying
. For a finite-difference eikonal solver such as FMM and
FSM, it is usually estimated by an upwind scheme during traveltime computations at each grid point
and thus can be easily extracted. Applying
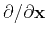 to both sides of
equation 3, we find
to both sides of
equation 3, we find
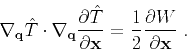 |
(6) |
Equation 6 has the form of the linearized eikonal equation (Aldridge, 1994) and was
previously derived, in a slightly different notation, by Alkhalifah and Fomel (2010). It implies that
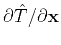 , as needed by equation 5, can be determined
along the characteristics of
, as needed by equation 5, can be determined
along the characteristics of 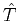 . Since the right-hand side contains a slowness-squared
derivative, the velocity model must be differentiable, as is usually required by traveltime
computations. The derivation also indicates that the accuracy of an eikonal-based traveltime
source-derivative is source-sampling independent but model-sampling dependent, as from equations
5 and 6
. Since the right-hand side contains a slowness-squared
derivative, the velocity model must be differentiable, as is usually required by traveltime
computations. The derivation also indicates that the accuracy of an eikonal-based traveltime
source-derivative is source-sampling independent but model-sampling dependent, as from equations
5 and 6
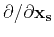 relies on
relies on
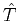 ,
,
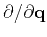 and
and
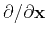 . The accuracy
from a direct finite-difference estimation on
. The accuracy
from a direct finite-difference estimation on
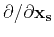 , in comparison,
is both source- and model-sampling dependent.
, in comparison,
is both source- and model-sampling dependent.
Continuing applying differentiation and the chain-rule to equation 5 will
result in higher-order traveltime source-derivatives. For example, the second-order
derivative reads:
Further, differentiating equation 6 once more by 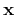 provides
provides
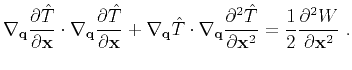 |
|
|
(8) |
It is easy to verify that any order of the traveltime source-derivative will require the
corresponding order of the slowness-squared derivative. An approximation based on Taylor
expansions of the traveltime around a fixed source location can make use of these derivatives.
For example, Ursin (1982) and Bortfeld (1989) introduced parabolic and hyperbolic traveltime
approximations with the first- and second-order derivatives. Notice that the need for slowness-squared
derivatives may cause instability unless the velocity model is sufficiently smooth. Alkhalifah and Fomel (2010)
also proved the following relationship between
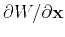 and
and
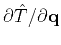 :
:
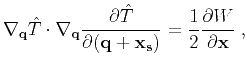 |
|
|
(9) |
which implies that the traveltime source-derivative can be computed from the given traveltime
tables only. However, the velocity smoothness is still implicitly assumed as the second-order spatial
derivatives of traveltimes appear in the equation. For this reason, we restrict our current implementation
to the first-order derivative only.
In a ray-tracing eikonal solver,
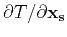 is the slowness vector
of a particular ray at
is the slowness vector
of a particular ray at 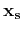 and holds constant along the trajectory. As it may also require
irregular coordinate mappings, one may use the same strategy as for the traveltime tables. In this way,
there is no necessity for any additional effort. On the other hand, equations 5 and
6 and their second-order extensions provide important attributes for use in Gaussian beams,
which are commonly calculated by the dynamic ray tracing (Cervený, 2001). They might be alternatively
estimated by the eikonal-based source-derivative formulas but with the traveltime tables from a
finite-difference eikonal solver. However, this application is beyond the scope of this paper. In the
following sections, we consider only the source-derivative estimation from traveltimes computed by a
finite-difference eikonal solver.
and holds constant along the trajectory. As it may also require
irregular coordinate mappings, one may use the same strategy as for the traveltime tables. In this way,
there is no necessity for any additional effort. On the other hand, equations 5 and
6 and their second-order extensions provide important attributes for use in Gaussian beams,
which are commonly calculated by the dynamic ray tracing (Cervený, 2001). They might be alternatively
estimated by the eikonal-based source-derivative formulas but with the traveltime tables from a
finite-difference eikonal solver. However, this application is beyond the scope of this paper. In the
following sections, we consider only the source-derivative estimation from traveltimes computed by a
finite-difference eikonal solver.
 |
 |
 |
 | Kirchhoff migration using eikonal-based computation of traveltime source-derivatives |  |
![[pdf]](icons/pdf.png) |
Next: Numerical Implementation
Up: Theory and Implementation
Previous: Theory and Implementation
2013-07-26
![]() clearly depends on the source location
clearly depends on the source location ![]() . To
explicitly show such a dependency in the eikonal equation, we define a relative coordinate
. To
explicitly show such a dependency in the eikonal equation, we define a relative coordinate ![]() as
as
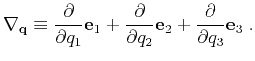
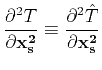
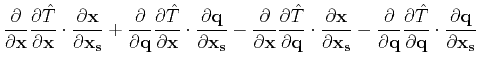
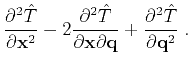
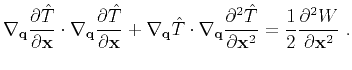
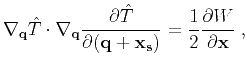
![]() is the slowness vector
of a particular ray at
is the slowness vector
of a particular ray at ![]() and holds constant along the trajectory. As it may also require
irregular coordinate mappings, one may use the same strategy as for the traveltime tables. In this way,
there is no necessity for any additional effort. On the other hand, equations 5 and
6 and their second-order extensions provide important attributes for use in Gaussian beams,
which are commonly calculated by the dynamic ray tracing (Cervený, 2001). They might be alternatively
estimated by the eikonal-based source-derivative formulas but with the traveltime tables from a
finite-difference eikonal solver. However, this application is beyond the scope of this paper. In the
following sections, we consider only the source-derivative estimation from traveltimes computed by a
finite-difference eikonal solver.
and holds constant along the trajectory. As it may also require
irregular coordinate mappings, one may use the same strategy as for the traveltime tables. In this way,
there is no necessity for any additional effort. On the other hand, equations 5 and
6 and their second-order extensions provide important attributes for use in Gaussian beams,
which are commonly calculated by the dynamic ray tracing (Cervený, 2001). They might be alternatively
estimated by the eikonal-based source-derivative formulas but with the traveltime tables from a
finite-difference eikonal solver. However, this application is beyond the scope of this paper. In the
following sections, we consider only the source-derivative estimation from traveltimes computed by a
finite-difference eikonal solver.