|
|
|
|
Quantifying and correcting residual azimuthal anisotropic moveout in image gathers using dynamic time warping |
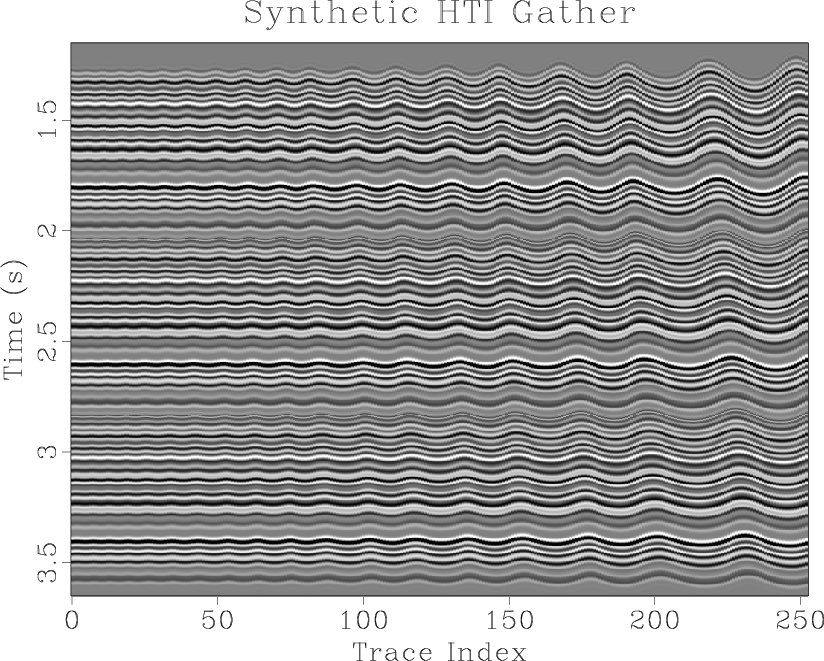
We use a synthetic example to demonstrate our method. Figure 3a contains an input synthetic spiral gather designed to simulate elliptical HTI anisotropy whose orientation and intensity vary with time. This gather is constructed by first taking a synthetic trace and spraying that trace into an ``ideal'' flat gather. Elliptical HTI effects are simulated by using normal moveout (NMO) modeling to generate a set of common azimuth gathers. Each of these gathers is modeled using a constant gradient velocity profile multiplied by an elliptic azimuthal anisotropy component in the form of Mallick et al. (1997) whose orientation varies with time. NMO correction using the constant gradient velocity profile is applied to each of the common azimuth gathers, leaving residual moveout from the unaccounted anisotropic component of the velocity profile. The spiral gather in Figure 3a is constructed from these common azimuth gathers by selecting appropriate offset and azimuth pairs. Although this spiral gather was constructed by applying isotropic NMO corrections to simulate an elliptical HTI medium, it effectively approximates HTI moveout in an image gather.
Notice that the periodicity of the elliptical HTI ``wiggles'' in the gather change with trace index as a result of irregular sampling of azimuth caused by the gather's spiral structure.
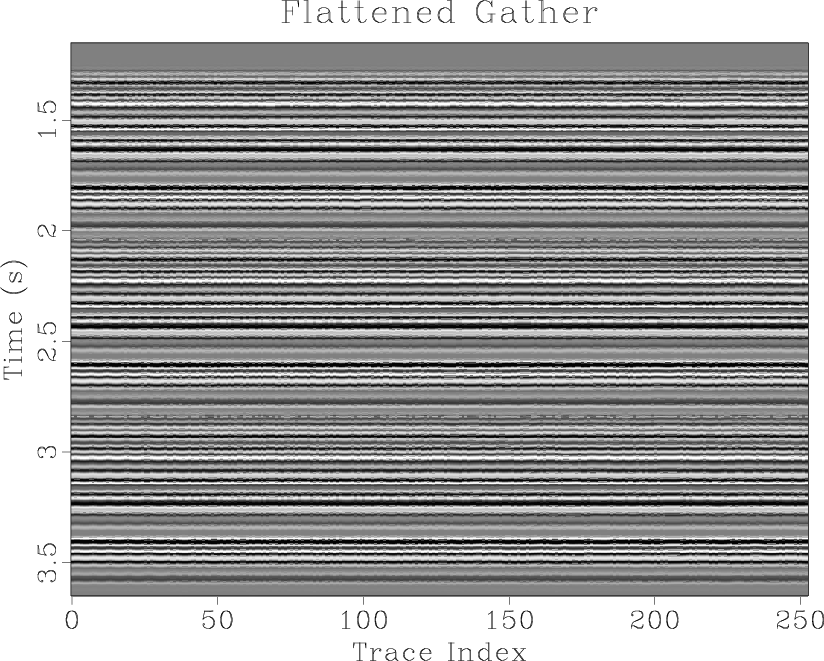
The input gather is stacked to create a reference trace, and DTW performed to determine the shifts which match each of the traces within the gather to the stack. To avoid cycle skipping, a strain limit is placed on the shifts so that they are unable to change too rapidly with time. These shifts are shown in Figure 3b. The blue bands, indicating the most negative shifts, correspond to the anisotropic principal, or fast, axis. The red bands indicate the anisotropic slow axis. The bands slope downward to the right, indicating the change of anisotropic axis orientation over time. The shifts in Figure 3b are applied to the traces in Figure 3a to generate the flattened gather shown in Figure 3c.


|
|---|
|
ex-nmo-slice,ex-gather-shifts,ex-flattened-gather,ex-gather-aniso
Figure 3. Synthetic example of dynamic time warping for gather flattening and determining principal anisotropic axis: (a) Synthetic gather with residual elliptical anisotropy; (b) Shifts that map the traces of Figure 3a to its stack; (c) Flattened gather resulting from applying the shifts in Figure 3b to the traces in Figure 3a; (d) Determining the principal HTI axis based on the shifts in Figure 3b. Background plots the value of equation 3 for different anisotropic azimuths. Solid yellow line plots the picked anisotropic azimuth which maximizes that equation at each time. Dotted blue line plots the ideal anisotropic azimuth. The difference between the maximizing and minimizing value of equation 3 at each time becomes the anisotropic intensity. |
|
|
To determine the orientation of the principal axis, we generate a suite of test functions according to equation 2 and integrate them against the gather shifts as described by equation 3. The result of this integral is plotted as the background color in Figure 3d. The maximum value of this integral is automatically picked at different times using the method described in Fomel (2009) and plotted as a solid yellow line in Figure 3d. This value provides ![]() , the anisotropic azimuth. The difference between the underlying value maximizing the integral and the minimizing value provides anisotropic intensity, a measure of the anisotropic ``wiggle'' size over the gather at that time. The ideal anisotropic azimuth is plotted as a dashed blue line in Figure 3d which overlays the picked anisotropy, indicating that the method has successfully recovered its value.
, the anisotropic azimuth. The difference between the underlying value maximizing the integral and the minimizing value provides anisotropic intensity, a measure of the anisotropic ``wiggle'' size over the gather at that time. The ideal anisotropic azimuth is plotted as a dashed blue line in Figure 3d which overlays the picked anisotropy, indicating that the method has successfully recovered its value.
We generate a series of stacks to illustrate the frequency content uplift resulting from gather flattening. Figure 4a contains a stack of the input gather from Figure 3a featuring residual elliptical HTI moveout. This stack is what traces are matched to during the dynamic warping process. Figure 4b plots the stack of the flattened gather from Figure 3c. Notice that this stack has higher frequency content than the input stack, where the residual elliptical HTI anisotropy has acted as a low-pass filter. For comparison, the stack of the ideal gather is shown in Figure 4c. This stack closely resembles that of the flattened gather, indicating that the gather flattening process has recovered high frequency information missing from the input gather's stack.



|
|---|
|
ex-nmo-slice-stk,ex-flattened-gather-stk,ex-flat-gather-stk
Figure 4. Stacks corresponding to: (a) the input gather in Figure 3a with residual elliptical HTI anisotropy; (b) the flattened gather in Figure 3c; (c) the ideal flat gather. |
|
|
|
|
|
|
Quantifying and correcting residual azimuthal anisotropic moveout in image gathers using dynamic time warping |