 |
 |
 |
 | Dip-separated structural filtering using seislet transform and adaptive empirical mode decomposition based dip filter |  |
![[pdf]](icons/pdf.png) |
Next: Conclusion
Up: Example
Previous: Synthetic example
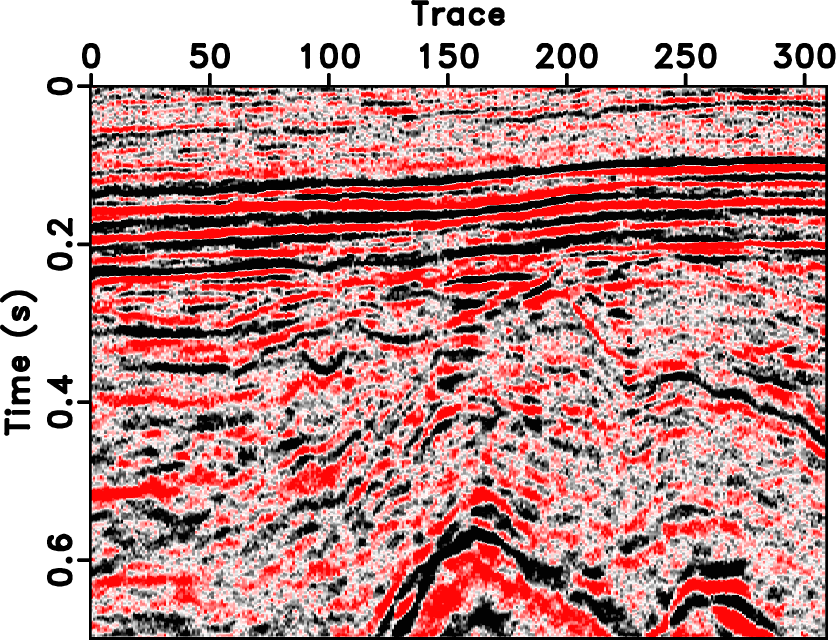
 deconvolution are shown in Figures 13d and 13e, respectively. The noise sections using four different approaches are shown in Figure 14. While the
deconvolution are shown in Figures 13d and 13e, respectively. The noise sections using four different approaches are shown in Figure 14. While the  deconvolution method fails to obtain acceptable result, the other three methods obtain much better performance in that seldom useful energy is damaged during the processing. However, it is obvious that the proposed approach remove the most random noise while preserving the useful signals. In this example, I preserve 10% coefficients in the seislet domain for each dip component, 14% coefficients in the seislet domain for the original image, and 20% coefficients in the curvelet domain. The comparisons of zoomed sections show more obvious advantage of the proposed approach in preserving more useful energy and enhancing weak signals that were smeared in traditional seislet method.
deconvolution method fails to obtain acceptable result, the other three methods obtain much better performance in that seldom useful energy is damaged during the processing. However, it is obvious that the proposed approach remove the most random noise while preserving the useful signals. In this example, I preserve 10% coefficients in the seislet domain for each dip component, 14% coefficients in the seislet domain for the original image, and 20% coefficients in the curvelet domain. The comparisons of zoomed sections show more obvious advantage of the proposed approach in preserving more useful energy and enhancing weak signals that were smeared in traditional seislet method.
The main cost in the proposed approach is the computation in the sifting process of empirical mode decomposition (Huang et al., 1998), which might require a large CPU cost. EMD process does not require a large memory cost since it is a recursive process and the memory required is in linear relation with the data size. The 3D version of the proposed approach may require a combination of 2D EMD along each frequency slice and a 3D version of seislet transform. Currently the proposed method is not applicable to 4D or 5D, since there are no 3D and 4D versions of EMD, or 4D and 5D versions of seislet transform.



|
|---|
field,field-emdseis,field-recon,field-ct,field-fx
Figure 13. (a) Field data. (b) Denoised data using the proposed approach. (c) Denoised data using the traditional seislet thresholding approach. (d) Denoised data using the curvelet transform. (e) Denoised data using  deconvolution. deconvolution.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|




|
|---|
field-emdseis-dif,field-seis-dif,field-ct-dif,field-fx-dif
Figure 14. Removed noise sections for field data. (a) Noise section using the proposed method. (b) Noise section using the conventional seislet thresholding method. (c) Noise section using the curvelet thresholding approach. (d) Noise section using  deconvolution. deconvolution.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|




|
|---|
zoom2-emdseis,zoom2-recon,zoom1-emdseis,zoom1-recon
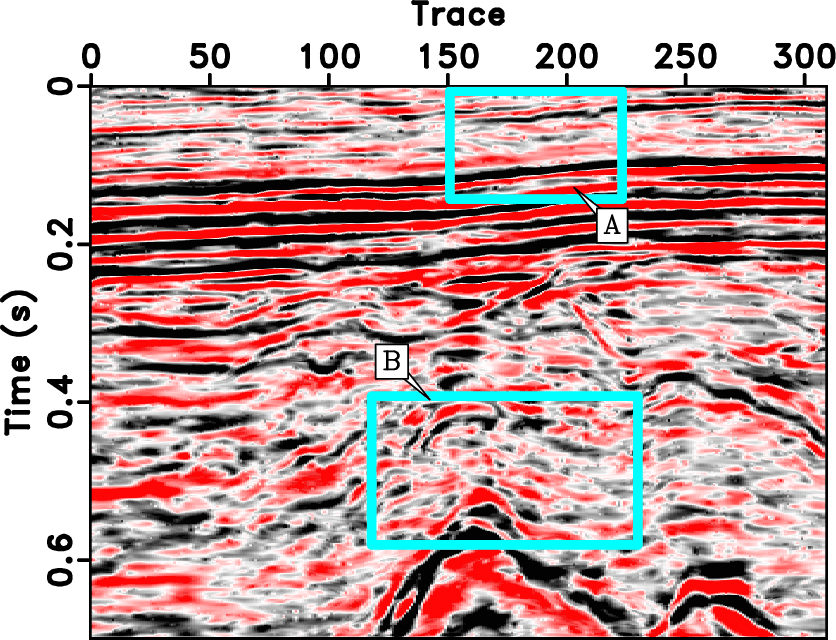
Figure 15. Zoomed denoised results for field data (corresponding to the frame boxes A & B in Figure 13). (a) & (c) correspond to the proposed method. (b) & (d) correspond to the conventional seislet thresholding method.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Dip-separated structural filtering using seislet transform and adaptive empirical mode decomposition based dip filter |  |
![[pdf]](icons/pdf.png) |
Next: Conclusion
Up: Example
Previous: Synthetic example
2020-02-28












