Iterative deblending of simultaneous-source seismic data using seislet-domain shaping regularization

Comparison of sparsity-promoting transforms

The best-known sparsity-promoting transforms are the Fourier and wavelet transform. Fomel and Liu (2010) proposed a sparsity-promoting transform called seislet transform. The specific adaptation for seismic data makes the seislet transform appealing to seismic data processing. In the seislet domain, useful events and blending noise reside at different scales and the useful signal tends to form a more compact regionWe provide a brief review of the seislet transform in Appendix A.

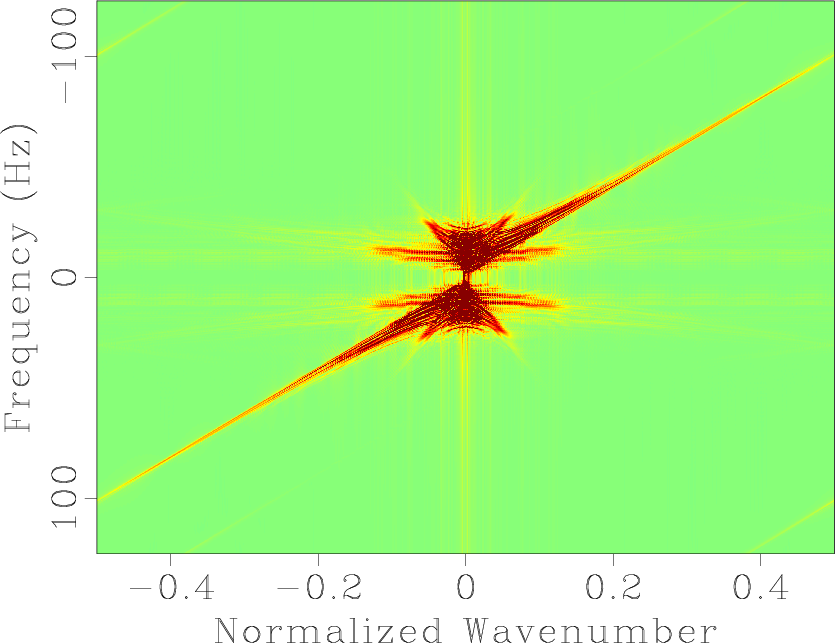
In order to illustrate the comparative sparseness of different transforms, we first create a simple synthetic data (Figure 1). Figure 2 shows different transformed domains for the data. Figure 2d shows a comparison between the decay of sorted coefficients in the 2-D Fourier transform, 2-D wavelet transform, and 2-D seislet transform. The 2-D Fourier transform in this case means the $f-k$ transform. The 2-D wavelet transform means implementing the 1-D wavelet transform along the temporal direction first and along the spatial direction second. The 2-D seislet transform means implementing the seislet transform along the spatial direction first and 1-D seislet transform along the temporal direction second. Our experiments show that the seislet coefficients decay significantly faster than coefficients of the other two transforms, which indicates a more compact structure of the seislet domain. The shaping operation is thus preferably chosen as the thresholding or mask operation in the seislet domain.

test1
Figure 1. A synthetic seismic profile.

ft,wlet,slet0,sigcoef
Figure 2. Comparison among different sparsity-promoting transforms. (a) 2-D Fourier transform domain. (b) 2-D Wavelet transform domain. (c) 2-D Seislet transform domain. (d) Coefficients decreasing diagram.

Iterative deblending of simultaneous-source seismic data using seislet-domain shaping regularization