|
|
|
|
Angle gathers in wave-equation imaging for transversely isotropic media |
We are grateful to KACST, KAUST, and the Bureau of Economic Geology, University of Texas at Austin for their support. We thank Gilles Lambare, Jeff Shragge and Jun Cao for their critical and helpful review of the paper.
![\begin{displaymath}\begin{array}{c} \frac{1}{2} \left(k_h^2-k_m^2\right)^4 \left...
... \eta +1) k_m^2-4 \omega ^2\right)^2\right)\right]^2\end{array}\end{displaymath}](img48.png)
|
|
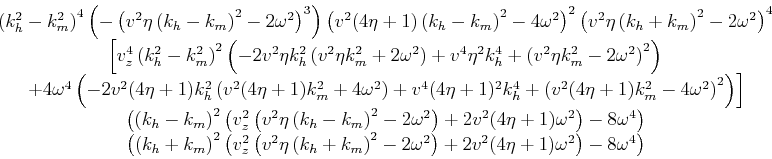
|
|
![\begin{displaymath}\begin{array}{c} \frac{1}{2} \left(k_h^2-k_m^2\right)^4 \left...
... \eta +1) k_m^2-4 \omega ^2\right)^2\right)\right]^2\end{array}\end{displaymath}](img48.png)
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
Angle gathers in wave-equation imaging for transversely isotropic media |