Angle gathers in wave-equation imaging for transversely isotropic media

Synthetic Example

In the following example, we use a homogeneous model for simplicity, although nothing in the development requires that. It is convenient so we can isolate the anisotropy influence on angle gathers decomposition. To follow convention, we display angle gathers in the following examples using half the opening (or scattering) angle ( $=\frac{\theta}{2}$ ). We consider the reflector model in Figure 6, which is made up of a number of dome-like anticlines. This model allows us to focus on an angle gather located at 8 km that includes many dips. For a velocity of 2 km/s and $\eta =0.2$ , we generate the prestack synthetic dataset shown in Figure 7. We use Kirchhoff modeling to obtain the synthetic data (Alkhalifah, 1995). As a reference, we show in Figure 8 the isotropic migration of the isotropic version of the data. In this figure, we observe the extension of reflections that are acquired with a limited offset in the angle representation.

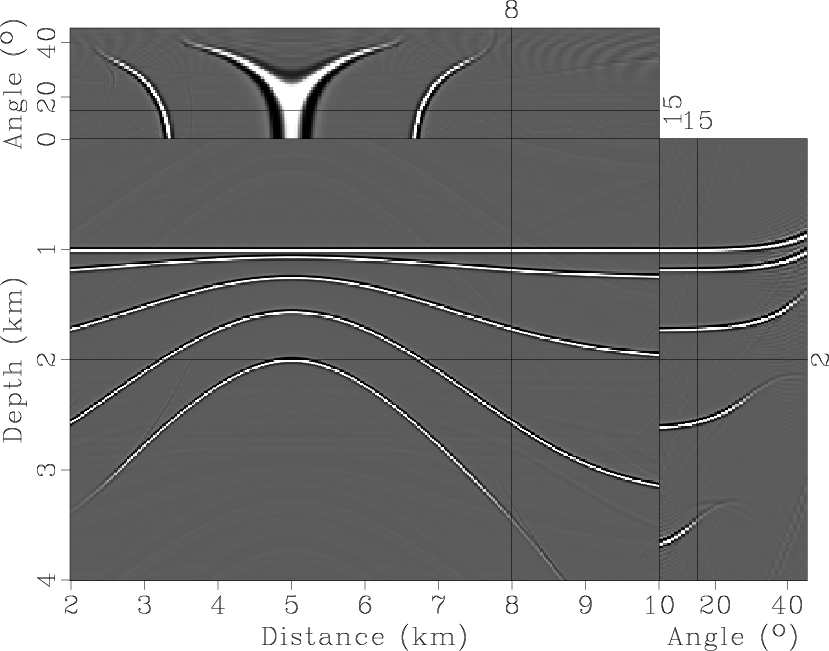
Conventional phase shift downward continuation requires that no lateral velocity variation is present. Since the synthetic model has no lateral (or even vertical) velocity variation, we use a VTI version of the DSR (double-square-root) phase-shift migration (Alkhalifah, 2000) to migrate the data. However, prior to applying the zero-time imaging condition we map the offset wavenumbers to angle, and thus, obtain angle gathers. Figure 9 shows the isotropically migrated section at near zero angle. It also shows on the right hand side the angle gather for an isotropic angle gather mapping. Clearly, the angle gather includes residuals resulting from ignoring anisotropy. These residuals start at the top with deviations at large angles with a fourth-order moveout (known as nonhyperbolic) often associated with the semi-horizontal reflectors to second-order strong deviations typically associated with dipping reflectors (Alkhalifah and Tsvankin, 1995). The top plot in Figure 9 is a slice of a constant depth of 2 km and includes some residual information spanning other angle gathers.

If we downward continue using an anisotropic phase-shift migration followed by an isotropic angle gather mapping, we image the data accurately as shown in Figure 10. Even the angle gathers, despite using an isotropic mapping, show no residuals as we have imaged that data accurately. However, though not immediately obvious, most of the migrated energy is mapped to the wrong angle. On the other hand, an anisotropic mapping of angle gathers places reflections at their true angles (Figure 11). This fact can be realized from comparing the extension of angle gathers of Figures 10 and 11. The lower-than-actual horizontal velocity treatment in the isotropic mapping places energy at smaller reflection angle values. This phenomenon can be directly attributed to the difference between phase and group velocities. Specifically, for horizontal reflections, the isotropic angle gathers map phase angles (ignoring the difference), while anisotropic ones map ray angles. When the horizontal velocity is higher in a VTI medium, the ray angle, measured from vertical, tend to be higher than the phase angle.

ref
Figure 6. A reflector model containing 5 reflections in a dome like formation. We focus on angle gathers at location 8 km, at which several reflection dips are represented.

adata
Figure 7. Prestack synthetic data generated using Kirchhoff modeling for a VTI model with velocity (NMO and vertical) equal 2 km/s and $\eta =0.2$ .

agath
Figure 8. Migrated section after an isotropic migration with velocity of 2 km/s of an equivalent isotropic synthetic data. The angle gathers obtained using an isotropic mapping at 8 km location is displayed on the right. The top section shows a depth slice as a function of angle gather at depth 2 km.

agath2
Figure 9. Migrated section after an isotropic migration with velocity of 2 km/s of the VTI synthetic data in Figure 7. Again, the angle gathers obtained using an isotropic mapping at 8 km location is displayed on the right, and the top section shows a depth slice as a function of angle gather at depth 2 km.

agath3
Figure 10. Migrated section after a VTI migration with velocity of 2 km/s and $\eta$ =0.2 of the VTI synthetic data in Figure 7. Again, the angle gathers obtained using an isotropic mapping at 8 km location is displayed on the right, and the top section shows a depth slice as a function of angle gather at depth 2 km.

agath4
Figure 11. Migrated section after a VTI migration with velocity of 2 km/s and $\eta$ =0.2 of the VTI synthetic data in Figure 7. The angle gathers obtained, now, using the VTI mapping at 8 km location is displayed on the right. The top section shows a depth slice as a function of angle gather at depth 2 km.

This synthetic test the importance of anisotropic angle gather mapping to place reflections at their true scattering angles. In practice, the velocity model building process uses residuals along angle gathers to estimate the required velocity update. Proper definition of the angle gather residuals will simplify the update process. This is especially true if the update is based on reflection tomography.

Angle gathers in wave-equation imaging for transversely isotropic media