 |
 |
 |
 | Solution steering with space-variant filters |  |
![[pdf]](icons/pdf.png) |
Next: Preconditioning
Up: THEORY/MOTIVATION
Previous: THEORY/MOTIVATION
In general, geophysical problems are ill-posed.
To obtain pleasing results we impose some type of regularization
criteria such as
diagonal scaling, limiting solutions to large
singular values (Clapp and Biondi, 1995), or
minimizing different solution norms (Nichols, 1994).
The
typical SEP approach is to minimize the power out of a regularization
operator (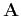 ) applied to the model (
) applied to the model (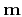 ),
described by the fitting goal
),
described by the fitting goal
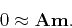 |
(1) |
Where 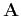 's spectrum will be the inverse of
's spectrum will be the inverse of 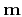 ,
so to produce a smooth
,
so to produce a smooth 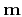 , we need a rough
, we need a rough
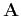 (Claerbout, 1994)).
The regularization operator can take many forms, in order of increasing
complexity:
(Claerbout, 1994)).
The regularization operator can take many forms, in order of increasing
complexity:
- Laplacian operator (
 )
)
- The symmetric nature of the
Laplacian leads to isotropic smoothing of the image.
- Steering filters
- Simple plane wave annihilation filters which
tend to orient the data in
some preferential direction,
chosen a priori. These filters can be simple two point filters,
Figure 1, to larger filters that sacrifice compactness for
more precise dip annihilation.
steering
Figure 1. An example of steering filter. In
this case preference is given to slopes at 45 degrees.
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[xfig]](icons/xfig.png)
|
|---|
- Prediction Error Filters (PEF)
- Like steering filters apply a
preferential smoothing direction, but are not limited to a single dip
and determine their smoothing directions
from the known data (Schwab, 1997).
 |
 |
 |
 | Solution steering with space-variant filters |  |
![[pdf]](icons/pdf.png) |
Next: Preconditioning
Up: THEORY/MOTIVATION
Previous: THEORY/MOTIVATION
2013-03-03
![]() ) applied to the model (
) applied to the model (![]() ),
described by the fitting goal
),
described by the fitting goal
