 |
 |
 |
 | Applications of plane-wave destruction filters |  |
![[pdf]](icons/pdf.png) |
Next: Application examples
Up: Fomel: Plane-wave destructors
Previous: High-order plane-wave destructors
Let us denote by
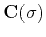 the operator of convolving the
data with the 2-D filter
the operator of convolving the
data with the 2-D filter 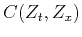 of equation (12),
assuming the local slope
of equation (12),
assuming the local slope
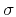 is known. In order to determine
the slope, we can define the least-squares goal
is known. In order to determine
the slope, we can define the least-squares goal
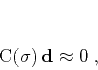 |
(13) |
where 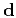 is the known data and the approximate equality
implies that the solution is found by minimizing the power of the
left-hand side. Equations (9) and (10) show that
the slope
is the known data and the approximate equality
implies that the solution is found by minimizing the power of the
left-hand side. Equations (9) and (10) show that
the slope
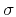 enters in the filter coefficients in an
essentially non-linear way. However, one can still apply the linear
iterative optimization methods by an analytical linearization of
equation (13). The linearization (also known as the Gauss-Newton
iteration) implies solving the linear system
enters in the filter coefficients in an
essentially non-linear way. However, one can still apply the linear
iterative optimization methods by an analytical linearization of
equation (13). The linearization (also known as the Gauss-Newton
iteration) implies solving the linear system
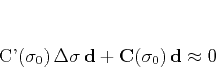 |
(14) |
for the slope increment
 . Here
. Here
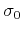 is the initial slope estimate, and
is the initial slope estimate, and
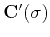 is a
convolution with the filter, obtained by differentiating the filter
coefficients of
is a
convolution with the filter, obtained by differentiating the filter
coefficients of
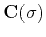 with respect to
with respect to
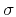 . After system (14) is solved, the initial
slope
. After system (14) is solved, the initial
slope
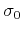 is updated by adding
is updated by adding
 to
it, and one can solve the linear problem again. Depending on the
starting solution, the method may require several non-linear
iterations to achieve an acceptable convergence.
to
it, and one can solve the linear problem again. Depending on the
starting solution, the method may require several non-linear
iterations to achieve an acceptable convergence.
The slope  in equation (14) does not have to be
constant. We can consider it as varying in both time and space
coordinates. This eliminates the need for local windows but may lead
to undesirably rough (oscillatory) local slope estimates. Moreover,
the solution will be undefined in regions of unknown or constant data,
because for these regions the local slope is not constrained. Both
these problems are solved by adding a regularization (styling) goal to
system (14). The additional goal takes the form
in equation (14) does not have to be
constant. We can consider it as varying in both time and space
coordinates. This eliminates the need for local windows but may lead
to undesirably rough (oscillatory) local slope estimates. Moreover,
the solution will be undefined in regions of unknown or constant data,
because for these regions the local slope is not constrained. Both
these problems are solved by adding a regularization (styling) goal to
system (14). The additional goal takes the form
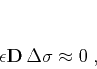 |
(15) |
where 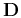 is an appropriate roughening operator and
is an appropriate roughening operator and 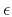 is a scaling coefficient. For simplicity, I chose
is a scaling coefficient. For simplicity, I chose 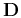 to be the
gradient operator. More efficient and sophisticated helical
preconditioning techniques are available
(Fomel, 2001; Claerbout, 1998; Fomel and Claerbout, 2002).
to be the
gradient operator. More efficient and sophisticated helical
preconditioning techniques are available
(Fomel, 2001; Claerbout, 1998; Fomel and Claerbout, 2002).
In theory, estimating two different slopes
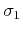 and
and
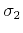 from the available data is only marginally more
complicated than estimating a single slope. The convolution operator
becomes a cascade of
from the available data is only marginally more
complicated than estimating a single slope. The convolution operator
becomes a cascade of
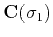 and
and
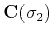 , and the linearization yields
, and the linearization yields
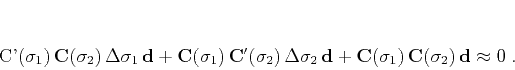 |
(16) |
The regularization condition should now be applied to both
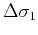 and
and
 :
:
The solution will obviously depend on the initial values of
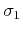 and
and
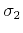 , which should not be equal to
each other. System (16) is generally underdetermined,
because it contains twice as many estimated parameters as equations:
The number of equations corresponds to the grid size of the data
, which should not be equal to
each other. System (16) is generally underdetermined,
because it contains twice as many estimated parameters as equations:
The number of equations corresponds to the grid size of the data
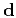 , while characterizing variable slopes
, while characterizing variable slopes 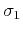 and
and
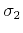 on the same grid involves two gridded functions. However,
an appropriate choice of the starting solution and the additional
regularization (17-18) allow us to arrive at a
practical solution.
on the same grid involves two gridded functions. However,
an appropriate choice of the starting solution and the additional
regularization (17-18) allow us to arrive at a
practical solution.
The application examples of the next section demonstrate that when the
system of equations (14-15)
or (16-18) are optimized in the least-squares
sense in a cycle of several linearization iterations, it leads to
smooth and reliable slope estimates. The regularization
conditions (15) and (17-18) assure
a smooth extrapolation of the slope to the regions of unknown or
constant data.
 |
 |
 |
 | Applications of plane-wave destruction filters |  |
![[pdf]](icons/pdf.png) |
Next: Application examples
Up: Fomel: Plane-wave destructors
Previous: High-order plane-wave destructors
2014-03-29
![]() the operator of convolving the
data with the 2-D filter
the operator of convolving the
data with the 2-D filter ![]() of equation (12),
assuming the local slope
of equation (12),
assuming the local slope
![]() is known. In order to determine
the slope, we can define the least-squares goal
is known. In order to determine
the slope, we can define the least-squares goal
![]() in equation (14) does not have to be
constant. We can consider it as varying in both time and space
coordinates. This eliminates the need for local windows but may lead
to undesirably rough (oscillatory) local slope estimates. Moreover,
the solution will be undefined in regions of unknown or constant data,
because for these regions the local slope is not constrained. Both
these problems are solved by adding a regularization (styling) goal to
system (14). The additional goal takes the form
in equation (14) does not have to be
constant. We can consider it as varying in both time and space
coordinates. This eliminates the need for local windows but may lead
to undesirably rough (oscillatory) local slope estimates. Moreover,
the solution will be undefined in regions of unknown or constant data,
because for these regions the local slope is not constrained. Both
these problems are solved by adding a regularization (styling) goal to
system (14). The additional goal takes the form
![]() and
and
![]() from the available data is only marginally more
complicated than estimating a single slope. The convolution operator
becomes a cascade of
from the available data is only marginally more
complicated than estimating a single slope. The convolution operator
becomes a cascade of
![]() and
and
![]() , and the linearization yields
, and the linearization yields