 |
 |
 |
 | Theory of differential offset continuation |  |
![[pdf]](icons/pdf.png) |
Next: Proof of amplitude equivalence
Up: Offset continuation geometry: time
Previous: Example 2: point diffractor
The third example (the right side of Figure 4) is the
curious case of a focusing elliptic reflector. Let  be the center
of the ellipse and
be the center
of the ellipse and  be half the distance between the foci of the
ellipse. If both foci are on the surface, the zero-offset
traveltime curve is defined by the so-called ``DMO smile''
(Deregowski and Rocca, 1981):
be half the distance between the foci of the
ellipse. If both foci are on the surface, the zero-offset
traveltime curve is defined by the so-called ``DMO smile''
(Deregowski and Rocca, 1981):
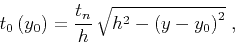 |
(40) |
where  , and
, and 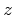 is the small semi-axis of the ellipse.
The time-ray equations are
is the small semi-axis of the ellipse.
The time-ray equations are
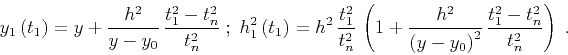 |
(41) |
When  coincides with
coincides with  , and
, and  coincides with
coincides with  , the
source and the receiver are in the foci of the elliptic reflector, and
the traveltime curve degenerates to a point
, the
source and the receiver are in the foci of the elliptic reflector, and
the traveltime curve degenerates to a point  . This remarkable
fact is the actual basis of the geometric theory of dip moveout
(Deregowski and Rocca, 1981).
. This remarkable
fact is the actual basis of the geometric theory of dip moveout
(Deregowski and Rocca, 1981).
 |
 |
 |
 | Theory of differential offset continuation |  |
![[pdf]](icons/pdf.png) |
Next: Proof of amplitude equivalence
Up: Offset continuation geometry: time
Previous: Example 2: point diffractor
2014-03-26
![]() be the center
of the ellipse and
be the center
of the ellipse and ![]() be half the distance between the foci of the
ellipse. If both foci are on the surface, the zero-offset
traveltime curve is defined by the so-called ``DMO smile''
(Deregowski and Rocca, 1981):
be half the distance between the foci of the
ellipse. If both foci are on the surface, the zero-offset
traveltime curve is defined by the so-called ``DMO smile''
(Deregowski and Rocca, 1981):