 |
 |
 |
 | Amplitude preservation for offset continuation:
Confirmation for Kirchhoff data |  |
![[pdf]](icons/pdf.png) |
Next: THE OFFSET CONTINUATION EQUATION
Up: Fomel & Bleistein: Offset
Previous: Introduction
In this section, we introduce the Kirchhoff approximate integral
representation of the upward propagating response to a single
reflector, with separated source and receiver points. We then show
how the amplitude of this integrand is related to the zero-offset
amplitude at the source receiver point on the ray, making equal angles
at the scattering point with the rays from the separated source and
receiver. The Kirchhoff integral representation (Bleistein, 1984; Haddon and Buchen, 1981)
describes the wavefield scattered from a single reflector. This
representation is applicable in situations where the high-frequency
assumption is valid (the wavelength is smaller than the characteristic
dimensions of the model) and corresponds in accuracy to the WKBJ
approximation for reflected waves, including phase shifts through
buried foci. The general form of the Kirchhoff modeling integral is
![\begin{displaymath}
U_S({\bf r,s, \omega}) = \int_\Sigma R ({\bf x;r,s})
{\pa...
...{\bf s, x ,\omega}) G({\bf x,r,\omega})\right]
d\Sigma \; ,
\end{displaymath}](img1.png) |
(1) |
where
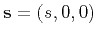 and
and
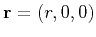 stand for the source
and the receiver location vectors at the surface of observation;
stand for the source
and the receiver location vectors at the surface of observation;  denotes a point on the reflector surface
denotes a point on the reflector surface  ;
;  is the
reflection coefficient at
is the
reflection coefficient at 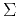 ;
;  is the upward normal to the
reflector at the point
is the upward normal to the
reflector at the point  ; and
; and 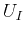 and
and 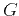 are the incident
wavefield and Green's function, respectively represented by their WKBJ
approximation,
are the incident
wavefield and Green's function, respectively represented by their WKBJ
approximation,
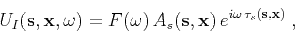 |
(2) |
 |
(3) |
In this equation,
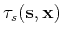 and
and
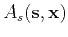 are the traveltime and the
amplitude of the wave propagating from
are the traveltime and the
amplitude of the wave propagating from 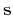 to
to  ;
;
 and
and
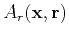 are the corresponding
quantities for the wave propagating from
are the corresponding
quantities for the wave propagating from  to
to  ; and
; and
 is the spectrum of the input signal, assumed to be
the transform of a bandlimited impulsive source.
In the time domain,
the Kirchhoff modeling integral transforms to
is the spectrum of the input signal, assumed to be
the transform of a bandlimited impulsive source.
In the time domain,
the Kirchhoff modeling integral transforms to
![\begin{displaymath}
u_S({\bf r,s},t) =
\int_\Sigma R ({\bf x;r,s}) {\partial ...
...u_s({\bf s,x}) - \tau_r({\bf x,r})\right)\right]
d{\bf x}\;,
\end{displaymath}](img19.png) |
(4) |
with  denoting the inverse temporal transform of
denoting the inverse temporal transform of 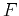 . The
reflection traveltime
. The
reflection traveltime  corresponds physically to the
diffraction from a point diffractor located at the point
corresponds physically to the
diffraction from a point diffractor located at the point  on
the surface
on
the surface 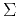 , and the amplitudes
, and the amplitudes  and
and  are point
diffractor amplitudes, as well.
are point
diffractor amplitudes, as well.
The main goal of this paper is to test the compliance of
representation (4) with the offset continuation differential
equation. The OC equation contains the derivatives of the wavefield
with respect to the parameters of observation (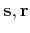 , and
, and
 ). According to the rules of classic calculus, these derivatives
can be taken under the sign of integration in formula
(4). Furthermore, since we do not assume that the true-amplitude
OC operator affects the reflection coefficient
). According to the rules of classic calculus, these derivatives
can be taken under the sign of integration in formula
(4). Furthermore, since we do not assume that the true-amplitude
OC operator affects the reflection coefficient 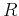 , the
offset-dependence of this coefficient is outside the scope of
consideration. Therefore, the only term to be considered as a trial
solution to the OC equation is the kernel of the Kirchhoff integral,
which is contained in the square brackets in equations (1) and
(4) and has the form
, the
offset-dependence of this coefficient is outside the scope of
consideration. Therefore, the only term to be considered as a trial
solution to the OC equation is the kernel of the Kirchhoff integral,
which is contained in the square brackets in equations (1) and
(4) and has the form
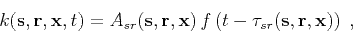 |
(5) |
where
 |
(6) |
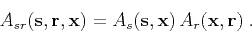 |
(7) |
In a 3-D medium with a constant velocity 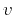 , the traveltimes and
amplitudes have the simple explicit expressions
, the traveltimes and
amplitudes have the simple explicit expressions
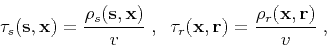 |
(8) |
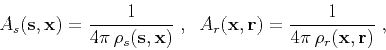 |
(9) |
where 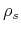 and
and 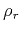 are the lengths of the incident and reflected
rays, respectively (Figure 1). If the reflector surface
are the lengths of the incident and reflected
rays, respectively (Figure 1). If the reflector surface
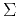 is explicitly defined by some function
is explicitly defined by some function  , then
, then
 |
(10) |

|
|---|
cwpgen
Figure 1. Geometry of diffraction in a
constant velocity medium: view in the reflection plane.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[xfig]](icons/xfig.png)
|
|---|
We then introduce a particular zero-offset amplitude, namely the
amplitude along the zero offset ray that bisects the angle between the
incident and reflected ray in this plane, as shown in Figure
1. We denote the square of this amplitude as  .
That is,
.
That is,
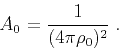 |
(11) |
 is the amplitude factor that appears in the Kirchhoff integral
set up for a zero-offset reflection along the ray
is the amplitude factor that appears in the Kirchhoff integral
set up for a zero-offset reflection along the ray 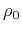 . It is,
thus, the desired output factor inside the Kirchhoff integral after
DMO. As follows from formulas (7) and
(9), the amplitude transformation in DMO (continuation to
zero offset) is characterized by the dimensionless ratio
. It is,
thus, the desired output factor inside the Kirchhoff integral after
DMO. As follows from formulas (7) and
(9), the amplitude transformation in DMO (continuation to
zero offset) is characterized by the dimensionless ratio
 |
(12) |
where 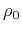 is the length of the zero-offset ray (Figure 1).
is the length of the zero-offset ray (Figure 1).
As follows from the simple trigonometry of the triangles, formed by
the incident and reflected rays (the law of cosines),
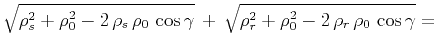 |
|
|
|
 |
|
|
(13) |
where  is the reflection angle, as shown in the figure.
After straightforward
algebraic transformations of equation (13), we arrive at the
explicit relationship between the ray lengths:
is the reflection angle, as shown in the figure.
After straightforward
algebraic transformations of equation (13), we arrive at the
explicit relationship between the ray lengths:
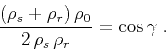 |
(14) |
Substituting (14) into (12) yields
 |
(15) |
where 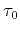 is the zero-offset two-way
traveltime (
is the zero-offset two-way
traveltime (
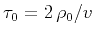 ).
).
What we have done is rewrite the finite-offset amplitude in the
Kirchhoff integral in terms of a particular zero-offset amplitude.
That zero-offset amplitude would arise as the geometric spreading
effect if there were a reflector whose dip was such that the
finite-offset pair would be specular at the scattering point. Of
course, the zero-offset ray would also be specular in this case.
 |
 |
 |
 | Amplitude preservation for offset continuation:
Confirmation for Kirchhoff data |  |
![[pdf]](icons/pdf.png) |
Next: THE OFFSET CONTINUATION EQUATION
Up: Fomel & Bleistein: Offset
Previous: Introduction
2013-03-03
![]() , and
, and
![]() ). According to the rules of classic calculus, these derivatives
can be taken under the sign of integration in formula
(4). Furthermore, since we do not assume that the true-amplitude
OC operator affects the reflection coefficient
). According to the rules of classic calculus, these derivatives
can be taken under the sign of integration in formula
(4). Furthermore, since we do not assume that the true-amplitude
OC operator affects the reflection coefficient ![]() , the
offset-dependence of this coefficient is outside the scope of
consideration. Therefore, the only term to be considered as a trial
solution to the OC equation is the kernel of the Kirchhoff integral,
which is contained in the square brackets in equations (1) and
(4) and has the form
, the
offset-dependence of this coefficient is outside the scope of
consideration. Therefore, the only term to be considered as a trial
solution to the OC equation is the kernel of the Kirchhoff integral,
which is contained in the square brackets in equations (1) and
(4) and has the form
![]() , the traveltimes and
amplitudes have the simple explicit expressions
, the traveltimes and
amplitudes have the simple explicit expressions

![]() .
That is,
.
That is,