The Wilson-Burg method of spectral factorization with application to helical filtering

Finite differences and spectral factorization

In the one-dimensional case, one finite-difference representation of the squared Laplacian is as a centered 5-point filter with coefficients $(1,-4,6,-4,1)$ . On the same grid, the Laplacian operator can be approximated to the same order of accuracy with the filter $(1/12,-4/3,5/2,-4/3,1/12)$ . Combining the two filters in accordance with equation (6) and performing the spectral factorization, we can obtain a 3-point minimum-phase filter suitable for inverse filtering. Figure 4 shows a family of one-dimensional minimum-phase filters for different values of the parameter $\lambda$ . Figure 5 demonstrates the interpolation results obtained with these filters on a simple one-dimensional synthetic. As expected, a small tension value ( $\lambda=0.01$ ) produces a smooth interpolation, but creates artificial oscillations in the unconstrained regions around sharp changes in the gradient. The value of $\lambda =1$ leads to linear interpolation with no extraneous inflections but with discontinuous derivatives. Intermediate values of $\lambda$ allow us to achieve a compromise: a smooth surface with constrained oscillations.

otens Figure 4. One-dimensional minimum-phase filters for different values of the tension parameter $\lambda$ . The filters range from the second derivative for $\lambda =0$ to the first derivative for $\lambda =1$ .

int
Figure 5. Interpolating a simple one-dimensional synthetic with recursive filter preconditioning for different values of the tension parameter $\lambda$ . The input data are shown on the top. The interpolation results range from a natural cubic spline interpolation for $\lambda =0$ to linear interpolation for $\lambda =1$ .

To design the corresponding filters in two dimensions, we define the finite-difference representation of operator (6) on a 5-by-5 stencil. The filter coefficients are chosen with the help of the Taylor expansion to match the desired spectrum of the operator around the zero spatial frequency. The matching conditions lead to the following set of coefficients for the squared Laplacian:

-1/60	2/5	7/30	2/5	-1/60
2/5	-14/15	-44/15	-14/15	2/5
7/30	-44/15	57/5	-44/15	7/30
2/5	-14/15	-44/15	-14/15	2/5
-1/60	2/5	7/30	2/5	-1/60

= 1/60

-1	24	14	24	-1
24	-56	-176	-56	24
14	-176	684	-176	14
24	-56	-176	-56	24
-1	24	14	24	-1

The Laplacian representation with the same order of accuracy has the coefficients

-1/360	2/45	0	2/45	-1/360
2/45	-14/45	-4/5	-14/45	2/45
0	-4/5	41/10	-4/5	0
2/45	-14/45	-4/5	-14/45	2/45
-1/360	2/45	0	2/45	-1/360

= 1/360

-1	16	0	16	-1
16	-112	-288	-112	16
0	-288	1476	-288	0
16	-112	-288	-112	16
-1	16	0	16	-1

For the sake of simplicity, we assumed equal spacing in the $x$ and $y$ direction. The coefficients can be easily adjusted for anisotropic spacing. Figures 6 and 7 show the spectra of the finite-difference representations of operator (6) for different values of the tension parameter. The finite-difference spectra appear to be fairly isotropic (independent of angle in polar coordinates). They match the exact expressions at small frequencies.

specc
Figure 6. Spectra of the finite-difference splines-in-tension schemes for different values of the tension parameter (contour plots).

specp
Figure 7. Spectra of the finite-difference splines-in-tension schemes for different values of the tension parameter (cross-section plots). The dashed lines show the exact spectra for continuous operators.

Regarding the finite-difference operators as two-dimensional auto-correlations and applying the Wilson-Burg method of spectral factorization, we obtain two-dimensional minimum-phase filters suitable for inverse filtering. The exact filters contain many coefficients, which rapidly decrease in magnitude at a distance from the first coefficient. For reasons of efficiency, it is advisable to restrict the shape of the filter so that it contains only the significant coefficients. Keeping all the coefficients that are $1000$ times smaller in magnitude than the leading coefficient creates a 53-point filter for $\lambda =0$ and a 35-point filter for $\lambda =1$ , with intermediate filter lengths for intermediate values of $\lambda$ . Keeping only the coefficients that are $200$ times smaller that the leading coefficient, we obtain 25- and 16-point filters for respectively $\lambda =0$ and $\lambda =1$ . The restricted filters do not factor the autocorrelation exactly but provide an effective approximation of the exact factors. As outputs of the Wilson-Burg spectral factorization process, they obey the minimum-phase condition.

splin
Figure 8. Inverse filtering with the tension filters. The left plots show the inputs composed of filters and spikes. Inverse filtering turns filters into impulses and turns spikes into inverse filter responses (middle plots). Adjoint filtering creates smooth isotropic shapes (right plots). The tension parameter takes on the values 0.3, 0.7, and 1 (from top to bottom). The case of zero tension corresponds to Figure 3.

Figure 8 shows the two-dimensional filters for different values of $\lambda$ and illustrates inverse recursive filtering, which is the essence of the helix method (Claerbout, 1998). The case of $\lambda =1$ leads to the filter known as helix derivative (Claerbout, 2002). The filter values are spread mostly in two columns. The other boundary case ($\lambda =0$ ) leads to a three-column filter, which serves as the minimum-phase version of the Laplacian. This filter is similar to the one shown in Figure 3. As expected from the theory, the inverse impulse response of this filter is noticeably smoother and wider than the inverse response of the helix derivative. Filters corresponding to intermediate values of $\lambda$ exhibit intermediate properties. Theoretically, the inverse impulse response of the filter corresponds to the Green's function of equation (6). The theoretical Green's function for the case of $\lambda =1$ is

$$G = \frac{1}{2\pi}\ln{r}\;,$$ (10)

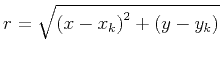where $r$ is the distance from the impulse: $r=\sqrt{\left(x-x_k\right)^2 + \left(y-y_k\right)}$ . In the case of $\lambda =0$ , the Green's function is smoother at the origin:

$$G = \frac{1}{8\pi}r^2\ln{r}\;.$$ (11)

The theoretical Green's function expression for an arbitrary value of $\lambda$ is unknown, but we can assume that its smoothness lies between the two boundary conditions.

In the next subsection, we illustrate an application of helical inverse filtering to a two-dimensional interpolation problem.

The Wilson-Burg method of spectral factorization with application to helical filtering