|
|
|
|
Angle-gather time migration |
|
rays
Figure 1. Reflection rays in a constant-velocity medium: a scheme. |

|
|---|---|
|
|
Let us consider a simple reflection experiment in an effectively
constant-velocity medium, as depicted in Figure 1. The
pair of incident and reflected rays and the line between the source
![]() and the receiver
and the receiver ![]() form a triangle in space. From the
trigonometry of that triangle we can derive simple relationships among
all the variables of the experiment
(Fomel, 1995,1996a,1997).
form a triangle in space. From the
trigonometry of that triangle we can derive simple relationships among
all the variables of the experiment
(Fomel, 1995,1996a,1997).
Introducing the dip angle ![]() and the reflection angle
and the reflection angle ![]() ,
the total reflection traveltime
,
the total reflection traveltime ![]() can be expressed from the law of
sines as
can be expressed from the law of
sines as
Additionally, by following simple trigonometry, we can connect the
half-offset ![]() with the depth of the reflection point
with the depth of the reflection point ![]() , as
follows:
, as
follows:
Finally, the horizontal distance between the midpoint ![]() and the
reflection point
and the
reflection point ![]() is
is
Equations (1-3) completely define the
kinematics of angle-gather migration. Regrouping the terms, we can
rewrite the three equations in a more symmetric form:
The lines of constant reflection angle ![]() and variable dip angle
and variable dip angle
![]() for a given position of a reflection (diffraction) point
for a given position of a reflection (diffraction) point
![]() have the meaning of summation curves for angle-gather
Kirchhoff migration. The whole range of such curves for all possible
values of
have the meaning of summation curves for angle-gather
Kirchhoff migration. The whole range of such curves for all possible
values of ![]() covers the diffraction traveltime surface -
``Cheops' pyramid'' (Claerbout, 1985) in the
covers the diffraction traveltime surface -
``Cheops' pyramid'' (Claerbout, 1985) in the ![]() space of seismic reflection data. As pointed out by
Fowler (1997), this condition is sufficient for proving the
kinematic validity of the angle-gather approach. For comparison,
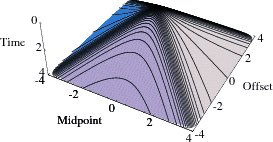
Figure 2 shows the diffraction traveltime pyramid from
a diffractor at 0.5 km depth. The pyramid is composed of
common-offset summation curves of the conventional time migration.
Figure 3 shows the same pyramid composed of
constant-
space of seismic reflection data. As pointed out by
Fowler (1997), this condition is sufficient for proving the
kinematic validity of the angle-gather approach. For comparison,
Figure 2 shows the diffraction traveltime pyramid from
a diffractor at 0.5 km depth. The pyramid is composed of
common-offset summation curves of the conventional time migration.
Figure 3 shows the same pyramid composed of
constant-![]() curves of the angle-gather migration.
curves of the angle-gather migration.
|
coffset
Figure 2. Traveltime pyramid, composed of common-offset summation curves. |

|
|---|---|
|
|
|
cangle
Figure 3. Traveltime pyramid, composed of common-reflection-angle summation curves. |
|
|---|---|
|
|
The most straightforward Kirchhoff algorithm of angle-gather migration can be formulated as follows:
|
|
|
|
Angle-gather time migration |