 |
 |
 |
 | Velocity-independent  -
- moveout
in a horizontally-layered VTI medium
moveout
in a horizontally-layered VTI medium |  |
![[pdf]](icons/pdf.png) |
Next: Stripping equations
Up: Estimation of interval parameters
Previous: Dix Inversion
Claerbout (1978) suggested that interval velocity in an
isotropic (
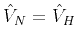 ) layered medium could be
estimated with a pen and a straightedge by measuring the
offset difference
) layered medium could be
estimated with a pen and a straightedge by measuring the
offset difference 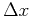 between equal slope
between equal slope  points on two
reflection events (Figure 1a). The computation of
points on two
reflection events (Figure 1a). The computation of 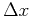 is straightforward after a CMP gather has been transformed into the
is straightforward after a CMP gather has been transformed into the
 -
- domain. In fact, the
domain. In fact, the  -
- transform naturally aligns seismic
events with equal slope along the same trace
(Figure 1b). Moreover, local slopes
transform naturally aligns seismic
events with equal slope along the same trace
(Figure 1b). Moreover, local slopes
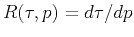 are
related to the emerging offset
are
related to the emerging offset 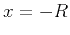 (van der Baan, 2004) , therefore
Claerbout's inversion formula can be expressed as
(van der Baan, 2004) , therefore
Claerbout's inversion formula can be expressed as
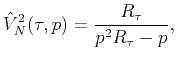 |
(23) |
where
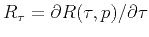 and
and  is the
NMO interval velocity that we map back to zero-slope time
is the
NMO interval velocity that we map back to zero-slope time  using the
isotropic velocity independent
using the
isotropic velocity independent  -
- NMO, as suggested by Fomel (2007b). The details of the derivation are in appendix C.
NMO, as suggested by Fomel (2007b). The details of the derivation are in appendix C.
The two methods discussed next can be thought of as two alternative
extensions for VTI media of the original Claerbout's straightedge
method.
 |
 |
 |
 | Velocity-independent  -
- moveout
in a horizontally-layered VTI medium
moveout
in a horizontally-layered VTI medium |  |
![[pdf]](icons/pdf.png) |
Next: Stripping equations
Up: Estimation of interval parameters
Previous: Dix Inversion
2011-06-25