 |
 |
 |
 | Velocity-independent  -
- moveout
in a horizontally-layered VTI medium
moveout
in a horizontally-layered VTI medium |  |
![[pdf]](icons/pdf.png) |
Next: Synthetic example of effective-parameter
Up: Casasanta & Fomel: Velocity-independent
Previous: The - domain
Under the quasi-acoustic approximation
(Alkhalifah, 1998,2000)
in a VTI homogeneous layer, the
vertical slowness 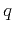 can be expressed as a function of the horizontal slowness
can be expressed as a function of the horizontal slowness  :
:
![$\displaystyle q(p)=\frac{1}{\hat{V}_{P0}}\sqrt{\dfrac{1-\hat{V}_{H}^{2}p^{2}}{1-[\hat{V}_{H}^{2}-\hat{V}_{N}^{2}]p^{2}}},$](img35.png) |
(5) |
where
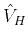 and
and
 are the horizontal and normal
moveout velocity in the layer. In the following equations, the
hat superscript
are the horizontal and normal
moveout velocity in the layer. In the following equations, the
hat superscript
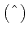 indicates layer or interval
parameters. Considering a stack of
indicates layer or interval
parameters. Considering a stack of 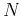 horizontal homogeneous layers
with horizontal symmetry planes, we can insert equation
5 into equation 4 to obtain an
expression for the
horizontal homogeneous layers
with horizontal symmetry planes, we can insert equation
5 into equation 4 to obtain an
expression for the  -
- reflection time from the bottom of the
reflection time from the bottom of the 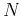 -th
layer, as follows:
-th
layer, as follows:
![$\displaystyle \tau (p)=\sum\nolimits_{n=1}^{N}\sqrt{\dfrac{1-\hat{V}_{H,n}^{2}p^{2}}{1-[\hat{V}_{H,n}^{2}-\hat{V}_{N,n}^{2}]p^{2}}}\Delta \tau _{0,n}$](img39.png) |
(6) |
where
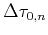 is the two way vertical time for the
is the two way vertical time for the 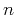 -th
layer. To simplify the following theoretical derivations, we assume
that, instead of having a layered velocity model, interval parameters
are vertically-varying continuous profiles. Therefore, we replace the
summation in formula 6 with an integral along
the vertical time
-th
layer. To simplify the following theoretical derivations, we assume
that, instead of having a layered velocity model, interval parameters
are vertically-varying continuous profiles. Therefore, we replace the
summation in formula 6 with an integral along
the vertical time  and arrive at the
following
and arrive at the
following  -
- moveout formula for a vertically-heterogeneous VTI
medium:
moveout formula for a vertically-heterogeneous VTI
medium:
![$\displaystyle \tau (p)=\displaystyle \int \limits_{0}^{\tau _{0}}\sqrt{ \dfrac{...
...^{2}(\xi )p^{2} } {1-[\hat{V}_{H}^{2}(\xi )-\hat{V}_{N}^{2}(\xi )]p^{2}}}d\xi ,$](img41.png) |
(7) |
where
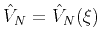 and
and
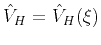 are (smooth) functions for interval
NMO and horizontal velocities, and
are (smooth) functions for interval
NMO and horizontal velocities, and  is the vertical
time. The vertical heterogeneity is measured as a function of
is the vertical
time. The vertical heterogeneity is measured as a function of  . The anellipticity parameter
. The anellipticity parameter
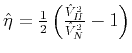 is also a function
of the vertical time
is also a function
of the vertical time  . Using effective parameters, equation 7 can be
approximated by
. Using effective parameters, equation 7 can be
approximated by
![$\displaystyle \tau (p)\approx \tau _{0}\sqrt{\dfrac{1-V_{H}^{2}(\tau _{0})p^{2}}{1-[V_{H}^{2}(\tau _{0})-V_{N}^{2}(\tau _{0})]p^{2}}},$](img47.png) |
(8) |
where the effective NMO 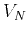 and horizontal
and horizontal 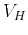 velocity are
related to the interval parameters through the second- and
fourth-order average velocities (Taner and Koehler, 1969; Ursin and Stovas, 2006) by the
following direct Dix-type formulas:
velocity are
related to the interval parameters through the second- and
fourth-order average velocities (Taner and Koehler, 1969; Ursin and Stovas, 2006) by the
following direct Dix-type formulas:
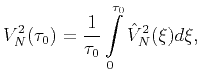 |
(9) |
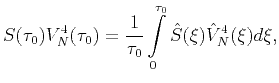 |
(10) |
where 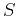 is the ratio between the fourth- and second-order
moments or the heterogeneity factor (Alkhalifah, 1997; Siliqi and Bousquié, 2000; de Bazelaire, 1988).
is the ratio between the fourth- and second-order
moments or the heterogeneity factor (Alkhalifah, 1997; Siliqi and Bousquié, 2000; de Bazelaire, 1988).
Equation 8 is basically the four-parameters rational approximation defined in  -
- domain Stovas and Fomel (2010)
domain Stovas and Fomel (2010)
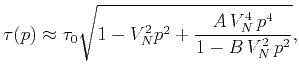 |
(11) |
with parameter 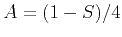 defined from the Taylor series
expansion of the exact
defined from the Taylor series
expansion of the exact  -
- function (Ursin and Stovas, 2006). Under
the acoustic VTI approximation,
function (Ursin and Stovas, 2006). Under
the acoustic VTI approximation, 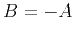 and the equation 11 now
depends on three parameters only. Finally, to be consistent with
equation 8, the heterogeneity coefficient becomes
and the equation 11 now
depends on three parameters only. Finally, to be consistent with
equation 8, the heterogeneity coefficient becomes
 . In principle, it is possible to use any
other three-parameters approximation in
. In principle, it is possible to use any
other three-parameters approximation in  -
- domain apart from the
rational approximation 11 like, for example, the
shifted ellipse approximation given by
Stovas and Fomel (2010). The reason for choosing the approximation
8 is that it accurately describes the
domain apart from the
rational approximation 11 like, for example, the
shifted ellipse approximation given by
Stovas and Fomel (2010). The reason for choosing the approximation
8 is that it accurately describes the  -
- moveout for a single VTI layer (blue line in figure
2b). Nevertheless, approximation
8 remains valid for vertically heterogeneous
VTI media with a decrease in accuracy for larger angles (large values
of
moveout for a single VTI layer (blue line in figure
2b). Nevertheless, approximation
8 remains valid for vertically heterogeneous
VTI media with a decrease in accuracy for larger angles (large values
of  ) because of the Dix averaging
) because of the Dix averaging
Letting  represent the slope
represent the slope
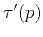 and
and  the curvature
the curvature
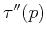 , we differentiate equation 8 once
, we differentiate equation 8 once
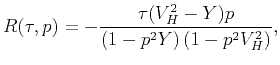 |
(12) |
and twice
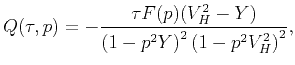 |
(13) |
where
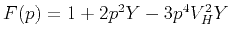 with
with
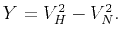 Equations 12 and 13 provide an
analytical description of the slope and curvature fields for given
effective values
Equations 12 and 13 provide an
analytical description of the slope and curvature fields for given
effective values 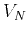 and
and 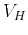 . Here we have omitted the
. Here we have omitted the
 dependency for clarity in the notation. Since
dependency for clarity in the notation. Since  -
- and
and  -
- domains are mapped by the linear transformation in equation
2, we observe that
domains are mapped by the linear transformation in equation
2, we observe that
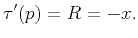 |
(14) |
Thus, the negative of the slope  has the physical meaning of
emerging offset, as pointed out by van der Baan (2004). Moreover, when the curvature
has the physical meaning of
emerging offset, as pointed out by van der Baan (2004). Moreover, when the curvature  changes sign, there is an inflection point in the
changes sign, there is an inflection point in the  -
- wavefront that is as a condition for caustics in
wavefront that is as a condition for caustics in  -
- domain. (Roganov and Stovas, 2011).
domain. (Roganov and Stovas, 2011).
Given slope  and curvature
and curvature  fields in a
fields in a  -
- CMP gather, we can eliminate the
velocity
CMP gather, we can eliminate the
velocity 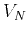 and the parameter
and the parameter 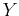 in equations 12
and 13, thus obtaining a ``
velocity-independent'' (Fomel, 2007b) moveout
equation in the
in equations 12
and 13, thus obtaining a ``
velocity-independent'' (Fomel, 2007b) moveout
equation in the  -
- domain:
domain:
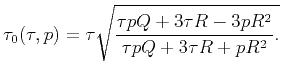 |
(15) |
Equation 15 describes a direct mapping from events
in the prestack  -
- data domain to zero-slope time
data domain to zero-slope time  . This
equation represents the oriented or slope-based moveout correction. As
follows from equations 12 and 13, the
effective parameters, if needed for other tasks, are given by the
following relations as a function of the slope and curvature estimates
(see Table 1):
. This
equation represents the oriented or slope-based moveout correction. As
follows from equations 12 and 13, the
effective parameters, if needed for other tasks, are given by the
following relations as a function of the slope and curvature estimates
(see Table 1):
and
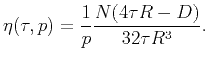 |
(18) |
In the above equations,
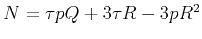 and
and
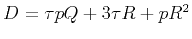 represent the terms in the numerator
represent the terms in the numerator 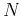 and denominator
and denominator 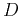 of the square root in equation 15. In the isotropic
or elliptically anisotropic case (
of the square root in equation 15. In the isotropic
or elliptically anisotropic case (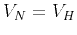 or
or 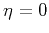 ), equations
15 to 18 simplify to equations
), equations
15 to 18 simplify to equations
 |
(19) |
and
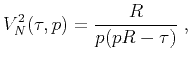 |
(20) |
previously published by Fomel (2007b).
The anisotropic parameters 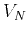 and
and 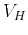 (or
(or  ) are no
longer a requirement for the moveout correction, as
in the case of conventional NMO processing, but
rather they are data attributes derived from local
slopes and curvatures. Moreover, these parameters are mappable
directly to the appropriate zero-slope time
) are no
longer a requirement for the moveout correction, as
in the case of conventional NMO processing, but
rather they are data attributes derived from local
slopes and curvatures. Moreover, these parameters are mappable
directly to the appropriate zero-slope time
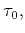 according to equation 15.
according to equation 15.
 |
 |
 |
 | Velocity-independent  -
- moveout
in a horizontally-layered VTI medium
moveout
in a horizontally-layered VTI medium |  |
![[pdf]](icons/pdf.png) |
Next: Synthetic example of effective-parameter
Up: Casasanta & Fomel: Velocity-independent
Previous: The - domain
2011-06-25
![]() can be expressed as a function of the horizontal slowness
can be expressed as a function of the horizontal slowness ![]() :
:
![]() and
and
![]() are the horizontal and normal
moveout velocity in the layer. In the following equations, the
hat superscript
are the horizontal and normal
moveout velocity in the layer. In the following equations, the
hat superscript
![]() indicates layer or interval
parameters. Considering a stack of
indicates layer or interval
parameters. Considering a stack of ![]() horizontal homogeneous layers
with horizontal symmetry planes, we can insert equation
5 into equation 4 to obtain an
expression for the
horizontal homogeneous layers
with horizontal symmetry planes, we can insert equation
5 into equation 4 to obtain an
expression for the ![]() -
-![]() reflection time from the bottom of the
reflection time from the bottom of the ![]() -th
layer, as follows:
-th
layer, as follows:
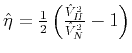 is also a function
of the vertical time
is also a function
of the vertical time ![]() -
-![]() domain Stovas and Fomel (2010)
domain Stovas and Fomel (2010)
 . In principle, it is possible to use any
other three-parameters approximation in
. In principle, it is possible to use any
other three-parameters approximation in ![]() represent the slope
represent the slope
![]() and
and ![]() the curvature
the curvature
![]() , we differentiate equation 8 once
, we differentiate equation 8 once
![]() and curvature
and curvature ![]() fields in a
fields in a ![]() -
-![]() CMP gather, we can eliminate the
velocity
CMP gather, we can eliminate the
velocity ![]() and the parameter
and the parameter ![]() in equations 12
and 13, thus obtaining a ``
velocity-independent'' (Fomel, 2007b) moveout
equation in the
in equations 12
and 13, thus obtaining a ``
velocity-independent'' (Fomel, 2007b) moveout
equation in the ![]() -
-![]() domain:
domain:
![]() -
-![]() data domain to zero-slope time
data domain to zero-slope time ![]() . This
equation represents the oriented or slope-based moveout correction. As
follows from equations 12 and 13, the
effective parameters, if needed for other tasks, are given by the
following relations as a function of the slope and curvature estimates
(see Table 1):
. This
equation represents the oriented or slope-based moveout correction. As
follows from equations 12 and 13, the
effective parameters, if needed for other tasks, are given by the
following relations as a function of the slope and curvature estimates
(see Table 1):
![]() and
and ![]() (or
(or ![]() ) are no
longer a requirement for the moveout correction, as
in the case of conventional NMO processing, but
rather they are data attributes derived from local
slopes and curvatures. Moreover, these parameters are mappable
directly to the appropriate zero-slope time
) are no
longer a requirement for the moveout correction, as
in the case of conventional NMO processing, but
rather they are data attributes derived from local
slopes and curvatures. Moreover, these parameters are mappable
directly to the appropriate zero-slope time
![]() according to equation 15.
according to equation 15.