|
|
|
|
A reversible transform for seismic data processing |
It is important to define a convention for the forward and inverse Fourier transform before proceeding. The shift-direction determined by the sign in a shifting exponential will reverse if the opposite sign convention for the Fourier transform is used. We use the forward Fourier transform convention,
In general, any processing step that requires a mapping from an input coordinate that is a function of the output coordinate, to that output coordinate, can be viewed as a nonstationary shift by combination. Examples of such processing steps include normal moveout (NMO), dip-moveout (DMO), and frequency-wavenumber (f-k) migration. NMO is a nonstationary shift in the time-space domain, while f-k migration performs a similar shift in the frequency-wavenumber domain. To remain general though, it is better at this point to think in terms of input and output coordinates rather than input and output times, so that frequency, wavenumber, space, or time shifts can be admitted, depending on the desired domain.
To emphasize that the input and output coordinates do not necessarily correspond to time, we use the above ![]() notation. A general nonstationary data processing shift in this notation is,
notation. A general nonstationary data processing shift in this notation is,
The forward transform given in 5 is in the mixed-domain.
For example, if the input function is defined over time, 5 takes the frequency spectrum of that input function, and outputs a new time series.
This should not be alarming, as the Fourier transform itself is a mixed-domain transform.
It may seem questionable how
![]() is handled in the exponent.
However, since the nonstationary shift is formulated here as a nonstationary combination, and the integration is over
is handled in the exponent.
However, since the nonstationary shift is formulated here as a nonstationary combination, and the integration is over ![]() , nothing new is needed to handle the relation between
, nothing new is needed to handle the relation between ![]() and
and ![]() .
.
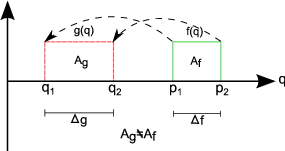
Although nonstationary combination kinematically performs nonstationary shifts correctly, amplitudes are not changed, and therefore energy is not conserved between input and output traces. Figure 1 demonstrates how the area under the input signal changes under a nonstationary combination shift. This nonphysical energy change within a trace is inherent to any processing step that applies or approximates a nonstationary shift. Rayleigh's theorem (also known as Plancherel's theorem) states that the integral of the square of an input function must be the same as the integral of its squared Fourier transform (Karl, 1989). Physically, this means that energy should be conserved between the input and Fourier domains, and clearly, the forward data processing transform violates this. Although nonphysical in most cases, nonstationary combination provides exactly the type of shift desired for the NMO correction and many other seismic data processing steps. The well-known issue of NMO stretch (Barnes, 1992) is a clear example of this type of energy change, where the seismic amplitudes remain unchanged after each trace has undergone the time-variant shift of the NMO correction. Relative to the input signal, this energy change means distortions in both the input and Fourier domains. These distortions are accounted for and handled by the inverse transform developed below, which relies on physically valid nonstationary convolution instead.
|
NSArea
Figure 1. Element area change caused by a nonstationary combination shift. The values of |
|
|---|---|
|
|
To quantify how the energy has been changed by the forward transform, take the ratio of areas of a shifted and unshifted rectangular element as in Figure 1:
Now that there is a mechanism for removing amplitude distortions, the rest of the inverse transform development comes from removing the kinematic shift.
The output function of the forward transform,
![]() , becomes the input function of the inverse transform.
Since the forward shift is applied simultaneously with the inverse Fourier transform, the reverse shift should be applied simultaneously with the forward Fourier transform. That is, the inverse data processing transform should naturally recover the original input spectrum,
, becomes the input function of the inverse transform.
Since the forward shift is applied simultaneously with the inverse Fourier transform, the reverse shift should be applied simultaneously with the forward Fourier transform. That is, the inverse data processing transform should naturally recover the original input spectrum,
![]() , rather than go directly back to the original input signal.
, rather than go directly back to the original input signal.
We first apply the Fourier transform to
![]() in terms of its own coordinate,
in terms of its own coordinate, ![]() , then reverse the nonstationary shift simultaneously,
, then reverse the nonstationary shift simultaneously,
The kinematics of this general data processing transform are clear under nonstationary filtering theory.
We claim that for any data processing step implemented by transform, the kinematics of the step can also be clearly understood, and that
![]() trivially predicts the amplitude corrections which are otherwise difficult to quantify using conventional filtering theory.
trivially predicts the amplitude corrections which are otherwise difficult to quantify using conventional filtering theory.
|
|
|
|
A reversible transform for seismic data processing |