 |
 |
 |
 | Velocity analysis using  semblance
semblance |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Fomel: Velocity analysis using
Previous: Apendix A: Statistical analysis
The problem of automatic picking of velocities from semblance scans
has been considered by many authors
(Adler and Brandwood, 1999; Arnaud et al., 2004; Siliqi et al., 2003). The
approach taken in this paper is inspired by the suggestion of
Harlan (2001) to look at velocity picking as a variational
problem. According to Harlan (2001), an optimally picked velocity trend
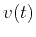 in the semblance field
in the semblance field
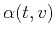 corresponds to the maximum
of the variational integral
corresponds to the maximum
of the variational integral
![$\displaystyle P_1[v(t)] = \int\limits_{t_{min}}^{t_{max}} \alpha\left(t,v(t)\right)\,d t\;.$](img48.png) |
(13) |
I take the variational formulation further by considering its
analogy to the ray tracing problem. The first-arrival seismic
ray is a trajectory corresponding to the minimum traveltime. The
trajectory corresponding to an optimal velocity trend should minimize
an analogous measure defined in the space of the velocity
scan  . I use the variational measure
. I use the variational measure
![$\displaystyle P_2[v(t)] = \int\limits_{t_{min}}^{t_{max}} \exp[-\alpha\left(t,v(t)\right)]\,\sqrt{\lambda^2+\left[v'(t)\right]^2}\,d t\;.$](img50.png) |
(14) |
where 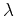 is a scaling parameter. According to variational theory
(Lanczos, 1966), an optimal trajectory can be determined by solving the eikonal equation
is a scaling parameter. According to variational theory
(Lanczos, 1966), an optimal trajectory can be determined by solving the eikonal equation
![$\displaystyle \left(\frac{\partial T}{\partial v}\right)^2 + \frac{1}{\lambda^2}\,\left(\frac{\partial T}{\partial t}\right)^2 = \exp[-2\,\alpha\left(t,v\right)]$](img52.png) |
(15) |
with a finite-difference algorithm. The quantity in the right hand
side of equation (B-3) plays the role of squared slowness.
Small slowness corresponds to high semblance and attracts ray
trajectories in a ``wave guide''. After obtaining a finite-difference
solution, the picking trajectory can be extracted by
tracking backward along the traveltime gradient direction. An
analogous approach has been used in medical imaging in the method of
virtual endoscopy (Deschamps and Cohen, 2001). To remove random oscillations, I
smooth the picked trajectory using the method of shaping
regularization
(Fomel, 2007).
 |
 |
 |
 | Velocity analysis using  semblance
semblance |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Fomel: Velocity analysis using
Previous: Apendix A: Statistical analysis
2013-03-02
![]() in the semblance field
in the semblance field
![]() corresponds to the maximum
of the variational integral
corresponds to the maximum
of the variational integral
![$\displaystyle P_1[v(t)] = \int\limits_{t_{min}}^{t_{max}} \alpha\left(t,v(t)\right)\,d t\;.$](img48.png)
![]() . I use the variational measure
. I use the variational measure
![$\displaystyle P_2[v(t)] = \int\limits_{t_{min}}^{t_{max}} \exp[-\alpha\left(t,v(t)\right)]\,\sqrt{\lambda^2+\left[v'(t)\right]^2}\,d t\;.$](img50.png)