 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Seismic-scale heterogeneities
Up: Statistical model of heterogeneities
Previous: Nonlinear parameter estimation on
O'Doherty and Anstey (1971) and Anstey and O'Doherty (2002a) described variations in
well logs by the superposition of different types of deposition,
leading to ``layers inside layers''. Their classification includes
- 1.
- A large number of small thickness layers (
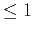 m)
for weakly transitional depositions with small reflection coefficients;
m)
for weakly transitional depositions with small reflection coefficients;
- 2.
- Cyclic layers of thicknesses from 1 to 10 m with sharp interfaces,
corresponding to fine layering depositions inside a facies
for short-period sea cycles; and
- 3.
- Horizons imaged by seismic reflection, i.e. different facies for a small number of thicker blocky layers associated with low-order cycles.
They suggested that transmission losses could be compensated by
multiple reflections, depending on seismic wavelength. This
classification is in agreement with the fact that high exponents, 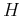 ,
appear for shorter scales,
,
appear for shorter scales,  , in Table 4. The
estimation performed on the sonic logs indicates fractal properties
for distances shorter than
, in Table 4. The
estimation performed on the sonic logs indicates fractal properties
for distances shorter than 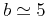 m. Acccording to
Anstey and O'Doherty (2002a), well log signals are the superposition of several
processes with different scales. The von Kármán model captures
part of it. Parameters extracted by our analysis describe
heterogeneities corresponding to type 2 of the O'Doherty-Anstey
classification, which is a fractal behavior inside major geological
units, at least from 10 down to 1 m, with a correlation length of 5 m.
Previous estimations of the correlation length on well logs were
produced by direct calculation of the spatial autocorrelation
(Shiomi et al., 1997; White et al., 1990). White et al. (1990) suggested the
possibility of superposition of two correlation lengths at 5 and 20 m.
The wavelet detection analysis of gamma-ray and resistivity well logs
for a sandstone confirmed the strong evidence of local cyclicity in
the stratigraphic sequences (Rivera et al., 2004). We think that
direct estimation of correlation distance
m. Acccording to
Anstey and O'Doherty (2002a), well log signals are the superposition of several
processes with different scales. The von Kármán model captures
part of it. Parameters extracted by our analysis describe
heterogeneities corresponding to type 2 of the O'Doherty-Anstey
classification, which is a fractal behavior inside major geological
units, at least from 10 down to 1 m, with a correlation length of 5 m.
Previous estimations of the correlation length on well logs were
produced by direct calculation of the spatial autocorrelation
(Shiomi et al., 1997; White et al., 1990). White et al. (1990) suggested the
possibility of superposition of two correlation lengths at 5 and 20 m.
The wavelet detection analysis of gamma-ray and resistivity well logs
for a sandstone confirmed the strong evidence of local cyclicity in
the stratigraphic sequences (Rivera et al., 2004). We think that
direct estimation of correlation distance  using the
autocorrelation function, or our estimation method, captures the
shortest dominant cycle in the sedimentary layers. This would explain
why the fractal behavior seems to hold for larger scales in
Figures 3(e) and 3(f).
using the
autocorrelation function, or our estimation method, captures the
shortest dominant cycle in the sedimentary layers. This would explain
why the fractal behavior seems to hold for larger scales in
Figures 3(e) and 3(f).
Parameter 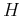 , estimated from well logs, is
, estimated from well logs, is 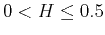 and
consistent with an antipersistent fractional Brownian motion characteristic of cyclicity (see Table 1).
The Hurst exponent commonly exhibits some antipersistence in sediments with values from 0.2
to 0.5 for sandstones (Lu et al., 2002; Dolan et al., 1998).
High values of 0.5 and 0.6 could be interpreted, in a clastic context,
to be caused by a transitional deposition involving persistency, as in natural floods.
Natural flood records exhibit a Hurst exponent,
and
consistent with an antipersistent fractional Brownian motion characteristic of cyclicity (see Table 1).
The Hurst exponent commonly exhibits some antipersistence in sediments with values from 0.2
to 0.5 for sandstones (Lu et al., 2002; Dolan et al., 1998).
High values of 0.5 and 0.6 could be interpreted, in a clastic context,
to be caused by a transitional deposition involving persistency, as in natural floods.
Natural flood records exhibit a Hurst exponent,
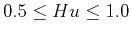 , associated
with so-called black noise (Mandelbrot and Wallis, 1969; Hurst, 1951).
, associated
with so-called black noise (Mandelbrot and Wallis, 1969; Hurst, 1951).
Subsections
 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Seismic-scale heterogeneities
Up: Statistical model of heterogeneities
Previous: Nonlinear parameter estimation on
2013-03-02
![]() , estimated from well logs, is
, estimated from well logs, is ![]() and
consistent with an antipersistent fractional Brownian motion characteristic of cyclicity (see Table 1).
The Hurst exponent commonly exhibits some antipersistence in sediments with values from 0.2
to 0.5 for sandstones (Lu et al., 2002; Dolan et al., 1998).
High values of 0.5 and 0.6 could be interpreted, in a clastic context,
to be caused by a transitional deposition involving persistency, as in natural floods.
Natural flood records exhibit a Hurst exponent,
and
consistent with an antipersistent fractional Brownian motion characteristic of cyclicity (see Table 1).
The Hurst exponent commonly exhibits some antipersistence in sediments with values from 0.2
to 0.5 for sandstones (Lu et al., 2002; Dolan et al., 1998).
High values of 0.5 and 0.6 could be interpreted, in a clastic context,
to be caused by a transitional deposition involving persistency, as in natural floods.
Natural flood records exhibit a Hurst exponent,
![]() , associated
with so-called black noise (Mandelbrot and Wallis, 1969; Hurst, 1951).
, associated
with so-called black noise (Mandelbrot and Wallis, 1969; Hurst, 1951).