 |
 |
 |
 | Signal and noise separation in prestack seismic data using velocity-dependent seislet transform |  |
![[pdf]](icons/pdf.png) |
Next: VD-slope pattern for pegleg
Up: Theory
Previous: Review of seislets
The kinematic description of a seismic event is an essential step for
several developments in seismic data processing. Local slope is
one important kinematic pattern for seismic data in the time-space
domain. PWD provides a constructive algorithm for estimating local slopes
(Chen et al., 2013b; Schleicher et al., 2009; Claerbout, 1992; Fomel, 2002; Chen et al., 2013a) and can
combine with a seislet framework to implement the PWD-seislet. Local
slant stack (Ottolini, 1983a) is another standard tool for
calculating slopes.
Under 1D earth assumption, one can consider the classic
hyperbolic model of primary reflection moveouts at near offsets
(Dix, 1955):
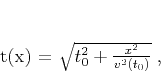 |
(6) |
where 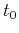 is the zero-offset traveltime,
is the zero-offset traveltime, 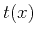 is the corresponding
primary traveltime recorded at offset
is the corresponding
primary traveltime recorded at offset  , and
, and 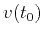 is the
stacking, or root mean square (RMS) velocity, which comes from a
standard velocity scan. As follows from equation 6, the
traveltime slopes
is the
stacking, or root mean square (RMS) velocity, which comes from a
standard velocity scan. As follows from equation 6, the
traveltime slopes 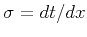 in CMP gathers are given by
in CMP gathers are given by
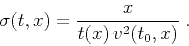 |
(7) |
This calculation is reverse to the one used in NMO by
velocity-independent imaging (Ottolini, 1983b; Fomel, 2007). To
calculate local slopes of primaries, we need to know 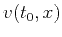 at
each time-space location (
at
each time-space location ( ). This can be accomplished by
simultaneously scanning both
). This can be accomplished by
simultaneously scanning both  and
and 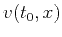 according to the
hyperbolic NMO equation at each
according to the
hyperbolic NMO equation at each  -coordinate position or by
time-warping. In this paper, we use the time-warping algorithm to calculate
-coordinate position or by
time-warping. In this paper, we use the time-warping algorithm to calculate
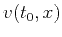 . Time warping performs mapping between different
coordinates: if one has sampled functions
. Time warping performs mapping between different
coordinates: if one has sampled functions 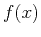 and
and 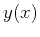 , the
mapping operation finds sampled
, the
mapping operation finds sampled 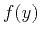 (Casasanta and Fomel, 2011; Burnett and Fomel, 2009).
(Casasanta and Fomel, 2011; Burnett and Fomel, 2009).
After the VD-slope pattern of primaries is calculated, we can design
pattern-based prediction and update operators 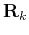 by using
plane-wave construction for the VD-seislet transform to represent only
primary reflections. When VD-seislet transform is applied to a CMP
gather, random noise spreads over different scales while the
predictable reflection information gets compressed to large
coefficients at small scales. A simple thresholding operation can easily
remove small coefficients. Finally, applying the inverse
VD-seislet transform reconstructs the signal while attenuating random
noise.
by using
plane-wave construction for the VD-seislet transform to represent only
primary reflections. When VD-seislet transform is applied to a CMP
gather, random noise spreads over different scales while the
predictable reflection information gets compressed to large
coefficients at small scales. A simple thresholding operation can easily
remove small coefficients. Finally, applying the inverse
VD-seislet transform reconstructs the signal while attenuating random
noise.
 |
 |
 |
 | Signal and noise separation in prestack seismic data using velocity-dependent seislet transform |  |
![[pdf]](icons/pdf.png) |
Next: VD-slope pattern for pegleg
Up: Theory
Previous: Review of seislets
2015-10-24
![]() by using
plane-wave construction for the VD-seislet transform to represent only
primary reflections. When VD-seislet transform is applied to a CMP
gather, random noise spreads over different scales while the
predictable reflection information gets compressed to large
coefficients at small scales. A simple thresholding operation can easily
remove small coefficients. Finally, applying the inverse
VD-seislet transform reconstructs the signal while attenuating random
noise.
by using
plane-wave construction for the VD-seislet transform to represent only
primary reflections. When VD-seislet transform is applied to a CMP
gather, random noise spreads over different scales while the
predictable reflection information gets compressed to large
coefficients at small scales. A simple thresholding operation can easily
remove small coefficients. Finally, applying the inverse
VD-seislet transform reconstructs the signal while attenuating random
noise.