3D - - streaming prediction filtering

Next: Data processing path in Up: Theory Previous: Theory

3D - - streaming prediction filtering

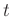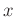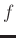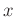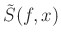A 2D seismic section containing linear events can be described as a plane wave function in the - domain. In the - domain, the linear events in seismic section $\tilde{S}(f,x)$ are decomposed into a series of sinusoids. These sinusoids are superimposed and become harmonics at each frequency, which shows the prediction relationship of seismic traces in a frequency slice:

$\displaystyle \sum_{p=1}^{P}a_{m,p}\tilde{S}_{m,n-p} = \tilde{S}_{m,n},$

(1)

where $m \in [1,M]$ and $n \in [1,N]$ are the indices of the seismic sample along the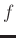

axis and

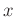axis, respectively. $p \in [1,P]$ is the index of filter coefficients along the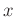

direction. $\tilde{S}_{m,n}$ denotes the data point in 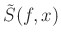$\tilde{S}(f,x)$ and $a_{m,p}$ indicates the filter coefficient in the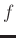

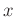domain. When curve events or amplitude-varying wavelets are shown in the seismic data, filter coefficients change from one data point to the next, which help to manage the nonstationary case:

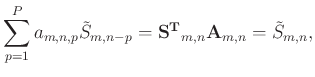$\displaystyle \sum_{p=1}^{P}a_{m,n,p}\tilde{S}_{m,n-p} = \mathbf{S^{T}}_{m,n} \mathbf{A}_{m,n} = \tilde{S}_{m,n},$

(2)

where $\{ \mathbf{T} \}$ denotes the transpose operator, $\mathbf{S}_{m,n}=[\tilde{S}_{m,n-1}, \\ \tilde{S}_{m,n-2}, \cdots, \tilde{S}_{m,n-p}]^{\mathbf{T}}$ denotes the vector including the data points near $\tilde{S}_{m,n}$ . $\mathbf{A}_{m,n}=[a_{m,n,1}, a_{m,n,2}, \cdots, a_{m,n,p}]^{\mathbf{T}}$ is the vector of coefficients in a 2D adaptive prediction filter. Let

, Fig. 1a illustrates how (2) works. Equation (2) denotes that the filter predicts data point along the spatial direction rather than the frequency direction. Therefore, an extension to the 3D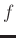

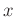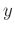domain is straightforward:

$\begin{equation*}\begin{aligned}& \sum_{p=-P}^{P}\sum_{q=-Q}^{Q}a_{m,n,l,p,q}\ti... ...}_{m,n,l} \quad (\vert p\vert+\vert q\vert \neq 0), \end{aligned}\end{equation*}$

where $l \in [1,L]$ is the index of the data sample along the

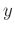axis. $p \in [-P,P]$ and $q \in [-Q,Q]$ are the indices of filter coefficients in two spatial directions, $\mathbf{A}_{m,n,l}=[a_{m,n,l,-P,-Q}, \cdots, a_{m,n,l,p,q}, \cdots, a_{m,n,l,P,Q}]^{\mathbf{T}}$ is the vector of 3D filter coefficients. The adaptive prediction filter $\mathbf{A}_{m,n,l}$ is defined as a space-noncausal structure and the filter size in the spatial direction is $(2P+1)\times(2Q+1)-1$ . The vector $\mathbf{S}_{m,n,l}= [\tilde{S}_{m,n+P,l+Q}, \cdots, \tilde{S}_{m,n-p,l-q}, \tilde{S}_{m,n-P,l-Q}]^{\mathbf{T}}$ contains the data points near $\tilde{S}_{m,n,l}$ . 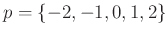Let $p=\{-2,-1,0,1,2\}$ and $q=\{-2,-1,0,1,2\}$ , Fig. 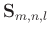2a demonstrates the distribution of the vectors $\mathbf{S}_{m,n,l}$ and $\mathbf{A}_{m,n,l}$ . Assuming that the contained noise is white Gaussian noise, the filter can be obtained by solving the minimization problem:

$\displaystyle \min_{\mathbf{A}_{m,n,l}} \left \Vert \mathbf{S^{T}}_{m,n,l} \mathbf{A}_{m,n,l} - \tilde{S}_{m,n,l} \right \Vert _{2}^{2},$

(4)

equation (4) describes an ill-posed problem that the number of the unknown filter coefficients is greater than that of the known equations. Without any regularization, the equation will lead to an unstable solution:

$\displaystyle \mathbf{A}_{LS}=(\mathbf{S^{*}}_{m,n,l} \mathbf{S^{T}}_{m,n,l})^{-1} \mathbf{S^{*}}_{m,n,l} \tilde{S}_{m,n,l},$

(5)

where $\{ * \}$ denotes the conjugate operator.

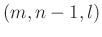To solve the underdetermined problem (4), constraint conditions based on local similarity/smoothness are used to stabilize the solution of (4). Assuming that the adaptive prediction filter at position is similar to another one at position in the 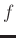- -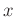 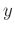domain, 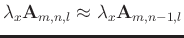$\lambda_{x} \mathbf{A}_{m,n,l} \approx \lambda_{x} \mathbf{A}_{m,n-1,l}$ can be treated as the constraint condition on the 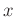axis. The autoregression equation can be expressed as follows:

$\begin{equation*}\begin{aligned}\begin{bmatrix}\tilde{S}_{m,n+P,l+Q} & \cdots & ... ...vdots \\ \lambda_{x} a_{m,n-1,l,P,Q} \end{bmatrix}, \end{aligned}\end{equation*}$

and the simplified block matrix can be written as:

$\displaystyle \begin{bmatrix}\mathbf{S^{T}}_{m,n,l} \\ \lambda_{x} \mathbf{I} \... ...in{bmatrix}\tilde{S}_{m,n,l} \\ \lambda_{x} \mathbf{A}_{m,n-1,l} \end{bmatrix}.$

(7)

Equation (7) is solvable since there are

equations with

unknown coefficients, which correspond to the following minimization problem:

$\displaystyle \min_{\mathbf{A}_{m,n,l}} \left \Vert \mathbf{S^{T}}_{m,n,l} \mat... ...2} \left \Vert \mathbf{A}_{m,n,l} - \mathbf{A}_{m,n-1,l} \right \Vert _{2}^{2},$

(8)

where $\lambda_{x}$ is the constant weight for the regularization term along the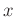

axis. In the frequency

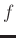direction, one can assume that the SPFs change smoothly and treat the irregular perturbations as the interference of noise. Meanwhile, the smoothness of the 3D SPFs also exists in different spatial directions and may change at different data point, therefore, we implemented local smoothness along

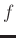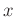, and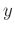

axis as constraints to calculate the

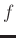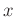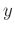SPF. The block matrix form is:

$\displaystyle \begin{bmatrix}\mathbf{S^{T}}_{m,n,l} \\ \lambda_{f}(m,n,l) \math... ...) \mathbf{A}_{m,n-1,l} \\ \lambda_{y}(m,n,l) \mathbf{A}_{m,n,l-1} \end{bmatrix}$

(9)

and the corresponding least-squares problem takes the following form:

$\begin{equation*}\begin{aligned}& \min_{\mathbf{A}_{m,n,l}} \left \Vert \mathbf{... ...,n,l} - \mathbf{A}_{m,n,l-1} \right \Vert _{2}^{2}, \end{aligned}\end{equation*}$

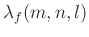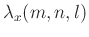where $\lambda_{f}(m,n,l)$ , $\lambda_{x}(m,n,l)$ and $\lambda_{y}(m,n,l)$ denotes the variable weights of regularization terms along the frequency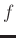

axis, space

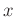axis, and space

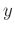axis, respectively. They measure the variable similarity or closeness between the filter $\mathbf{A}_{m,n,l}$ and the adjacent filters $\mathbf{A}_{m-1,n,l}$ , $\mathbf{A}_{m,n-1,l}$ , and $\mathbf{A}_{m,n,l-1}$ . Due to the prediction filter can characterize the energy spectrum of the input data Claerbout (1976), the adaptive filter shares analogical smoothness property with the 3D data, so the variation of the weights may consist with the smooth version of data. For simplicity, we select these weights with constant value, $\lambda_{f}(m,n,l) = \lambda_{f}$ , $\lambda_{x}(m,n,l) = \lambda_{x}$ and $\lambda_{y}(m,n,l) = \lambda_{y}$ , to demonstrate the constrained relationship. The introduced regularization terms convert the ill-posed problem to the overdetermined inverse problem, and the least-squares solution of (9) and (10) is:

$\begin{equation*}\begin{aligned}\mathbf{A}_{m,n,l} & = [ (\lambda_{f}^{2} + \lam... ...m,n,l} + \tilde{S}_{m,n,l} \mathbf{S^{*}}_{m,n,l}). \end{aligned}\end{equation*}$

where

$\begin{displaymath}\begin{cases}\lambda^{2} = \lambda_{f}^{2} + \lambda_{x}^{2} ... ...ambda_{y}^{2} \mathbf{A}_{m,n,l-1} ) / \lambda^{2}. \end{cases}\end{displaymath}$

(12)

The Sherman-Morrison formula is an analytic method for solving the inverse matrix Hager (1989):

$\displaystyle ( \lambda^{2}\mathbf{I} + \mathbf{S^{*}}_{m,n,l} \mathbf{S^{T}}_{... ...T}}_{m,n,l} } { \lambda^{2} + \mathbf{S^{T}}_{m,n,l} \mathbf{S^{*}}_{m,n,l} }).$

(13)

The derivation of the Sherman-Morrison formula in the complex space is described in Appendix

. Elementary algebraic simplifications lead to the analytical solution:

$\begin{equation*}\begin{aligned}\mathbf{A}_{m,n,l} & = ( \lambda^{2} \mathbf{I} ... ...} \mathbf{S^{*}}_{m,n,l} } \mathbf{ S^{*}}_{m,n,l}, \end{aligned}\end{equation*}$

Equation (14) is a recursion equation, which suggests that the filter $\mathbf{A}_{m,n,l}$ recursively updates in a certain order. The residual can be written as:

$\displaystyle r_{m,n,l}= \lambda^{2} \frac{ \tilde{S}_{m,n,l} - \mathbf{S^{T}}_... ...{A}}_{m,n,l} } { \lambda^{2} + \mathbf{S^{T}}_{m,n,l} \mathbf{S^{*}}_{m,n,l} }.$

(15)

Once obtaining the solution of the 3D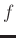

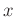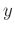SPF, one can compute the noise-free data $\tilde{X}_{m,n,l}$ with the following equation:

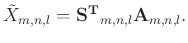$\displaystyle \tilde{X}_{m,n,l} = \mathbf{S^{T}}_{m,n,l} \mathbf{A}_{m,n,l}.$

(16)

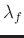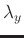The configuration of parameters $\lambda_{f}$ , $\lambda_{x}$ , and $\lambda_{y}$ is the basis for the proposed method. When the three parameters are 0 , the corresponding regularization terms have no effect on restricting the inverse problem and the result of the

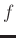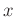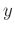SPF becomes (5). By choosing $\lambda_{y} = 0$ and removing the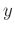

axis, equation (14) is reduced to the solution of the 2D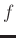

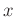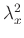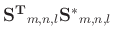SPF. On the contrary, when the three parameters tend to infinity, more weight is applied on regularization terms. A large denominator in (14) indicates that the filter cannot receive any updates to maintain its adaptive and predictive properties. This denominator suggests that parameters $\lambda_{x}^{2}$ and $\lambda_{y}^{2}$ in (12) should have the same order of magnitude as $\mathbf{S^{T}}_{m,n,l}\mathbf{S^{*}}_{m,n,l}$ , and the value of 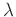$\lambda$ might be in the range of $(0, 10*\sqrt{ \max( \mathbf{S^{T}}_{m,n,l}\mathbf{S^{*}}_{m,n,l}) })$ , which can balance the noise suppression and signal protection. Therefore, they can smoothly adjust the change of filters. 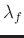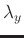Meanwhile, data distribution in the frequency axis may change sharply, which is not as smooth as those in the spatial directions; thus, $\lambda_{f}$ should be smaller than $\lambda_{x}$ and $\lambda_{y}$ .

**Table 1:** Cost comparison between 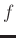- -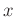 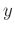RNA and 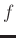- -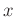 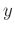SPF.
$\begin{threeparttable} \begin{tabular}{\vert c\vert c\vert c\vert} \hline & S... ... $N_{iter}$\ is the number of iterations. \end{tablenotes} \end{threeparttable}$


fig1,fig2 Figure 1. Schematic illustration of 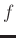- 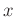prediction filter (a) and filter processing path (b).


fig3,fig4 Figure 2. Schematic illustration of 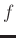- -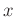 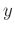prediction filter (a) and filter processing path in each frequency slice (b).

Next: Data processing path in Up: Theory Previous: Theory

2022-04-21