Next: Conclusion Up: Zheng et al.: Interpolation Previous: 3D data interpolation using

Discussion

We first discussed the value selection of the weights $\lambda_{f}$ , $\lambda_{x}$ , and $\lambda_{y}$ . Currently, we considered them as empirical parameters, but there are still some ways to determine their value range. 1) In Eq. (10) and (16), $\lambda^2$ and $\mathbf{G}_{m,n,l}^{\mathsf{T}}\mathbf{G}_{m,n,l}^{*}$ (or $\mathbf{G}_{m,n}^{\mathsf{T}}\mathbf{G}_{m,n}^{*}$ ) are the denominator of the filter update term. It is expected that $\lambda^{2}$ can influence the filter update, so $\lambda^2$ and $\mathbf{G}_{m,n,l}^{\mathsf{T}}\mathbf{G}_{m,n,l}^{*}$ (or $\mathbf{G}_{m,n}^{\mathsf{T}}\mathbf{G}_{m,n}^{*}$ ) should have a similar order of magnitude, where $\lambda^{2} = \lambda_{f}^{2}+\lambda_{x}^{2}+\lambda_{y}^{2}$ (or $\lambda^{2} = \lambda_{f}^{2}+\lambda_{x}^{2}$ ). 2) In terms of the prediction filtering theory in the frequency domain, the filter predicts the data sample along the spatial direction, not along the frequency direction. $\lambda_{x}$ and $\lambda_{y}$ in the spatial direction should be similar, and their values can be scaled according to the size of dataset. $\lambda_{f}$ mainly stabilizes the filter in the frequency direction, and it generally smaller than $\lambda_{x}$ and $\lambda_{y}$ . 3) The regularization terms' weight affect the data interpolation result to a certain extent. The values of $\lambda_{f}$ , $\lambda_{x}$ , and $\lambda_{y}$ can be set according to the previous method, and then they can be adjusted according to the interpolation effect.

For the case of regular decimation, we tested the synthetic 2D and 3D model in Fig. 19 and 20. In the 2D case, we used ten seismic traces to initialize the - SPF, in which the filter could reconstruct the missing data. As shown in Fig. 19b, the artifacts affect the data interpolation quality for traces with large slope differences between the seismic events. For the 3D data (Fig. 20), the - - SPF can directly recover the missing traces. Although the regular decimation of the 3D model has strong spatial aliasing, we still obtained a reasonable interpolation result.


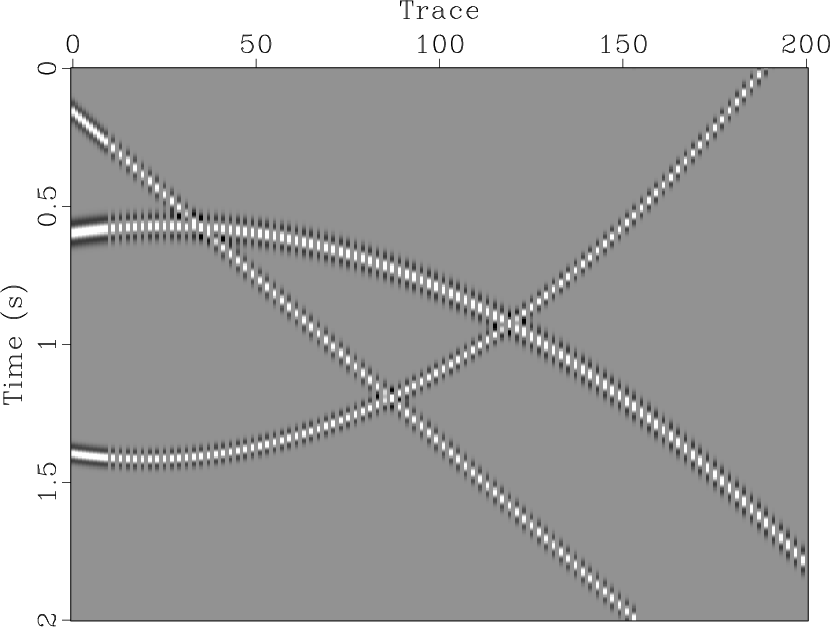
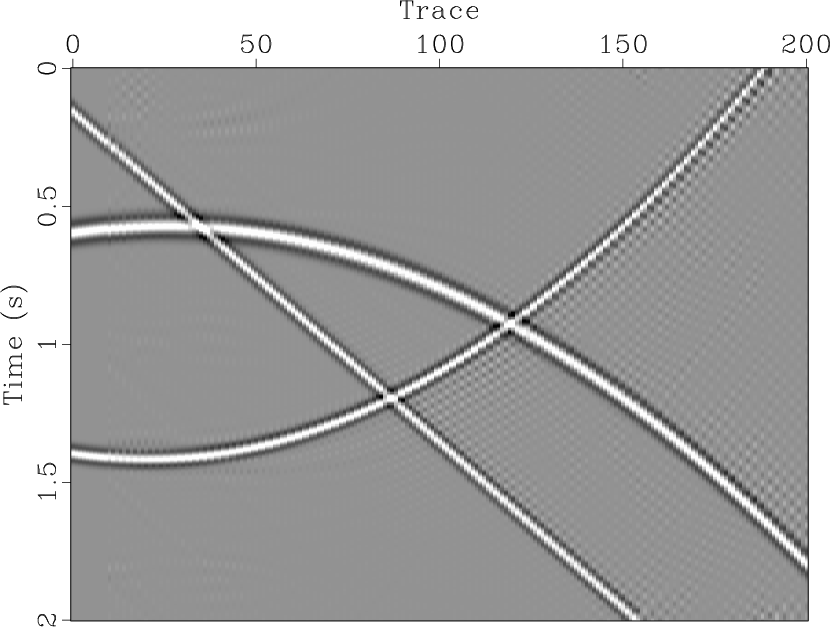
alias,intp Figure 19. Regular decimation of synthetic 2D model (a), and interpolated result using the 2D - SPF (b).


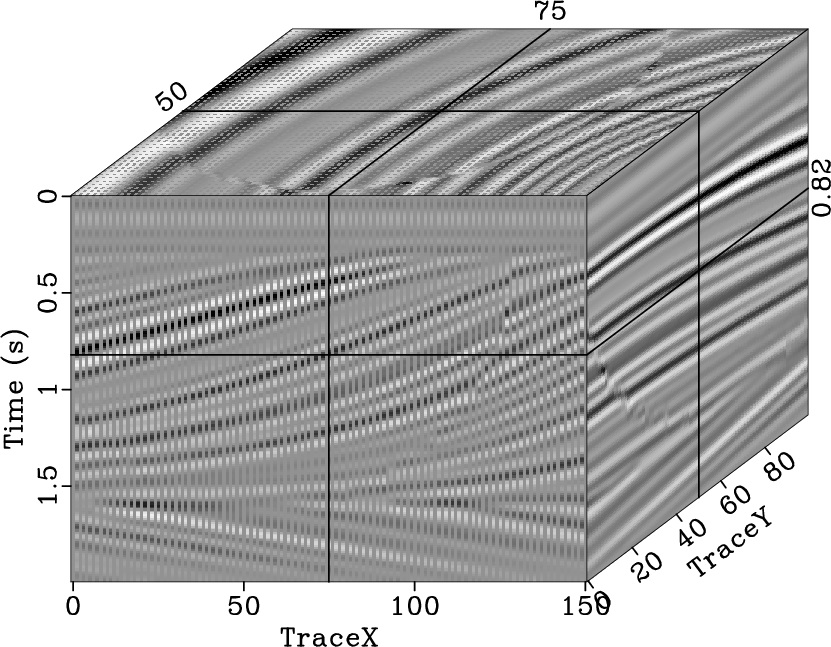
aliasqd,intpqd Figure 20. Regular decimation of synthetic 3D model (a), and interpolated result using the 3D - - SPF (b).

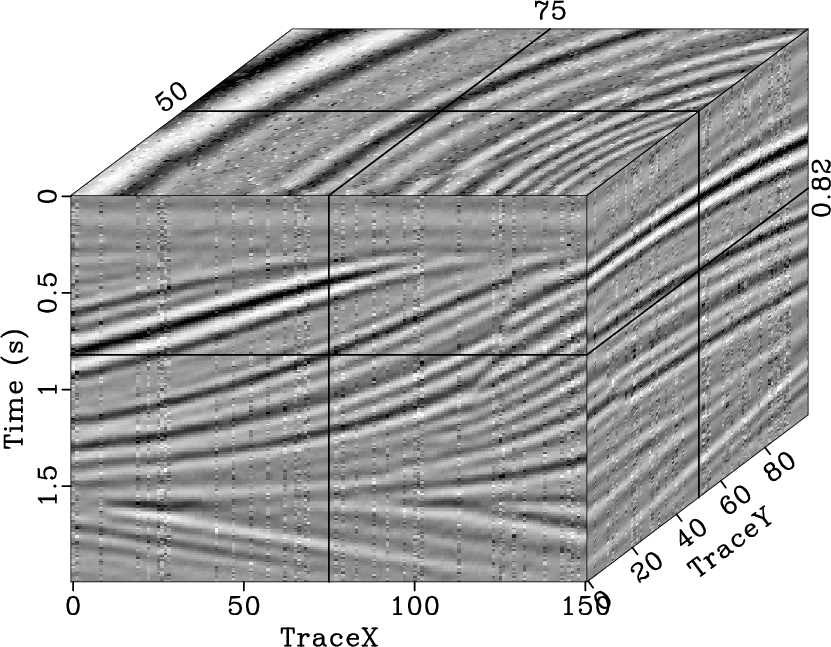
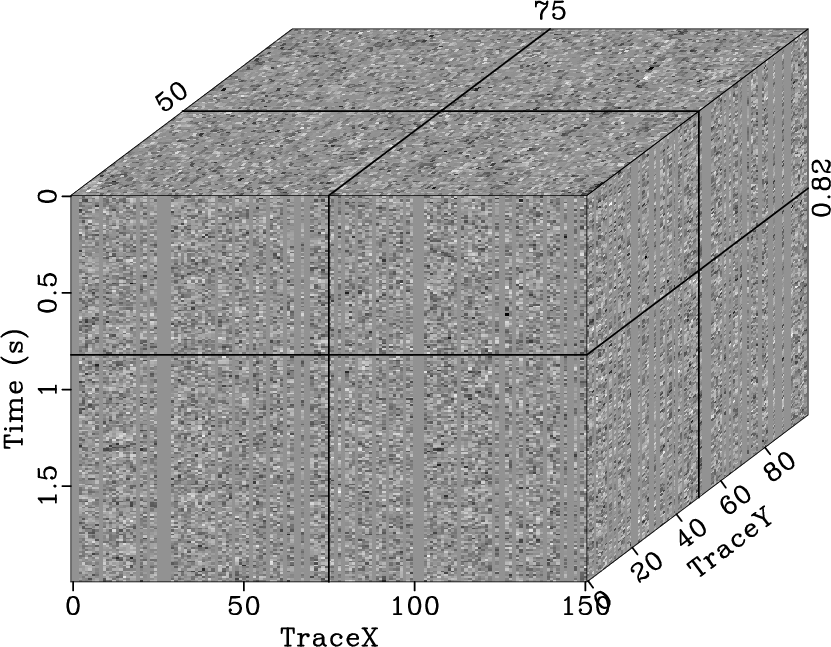
We also tested the effectiveness of the proposed method in the case of low SNR. We added stronger noise to both the 2D and 3D synthetic model (Fig. 21a and 23a), which both had randomly decimated seismic traces. The strong random noise influenced the local slope calculation, which further affected the seislet transform. By using the 2D seislet POCS, the interpolation result of the 2D model (Fig. 22a and 22b) shows some smearing, and the 3D model cannot be reconstructed (Fig. 24a and 24b). For the 2D Fourier POCS method, there are some parts of the upward curve that are not recovered in the 2D model (Fig. 22c and 22d). Additionally, the 3D Fourier POCS method produces a reasonable reconstruction result (Fig. 24c), although leakage signal of the seismic events presents in the interpolation error profile (Fig. 24d). Because the PF can be used to attenuate random noise, and it may reduce the impact of random noise to some extent, our proposed methods (the - SPF and the - - SPF) yield better reconstruction results (Fig. 22e, 22f, 24e, and 24f) under low SNR than other methods.


noisemod,noisegap Figure 21. Synthetic model with random noise (a), model with 40% of the data traces randomly removed (b).


noisestpocs,noiseerrstpocs,noisepocs,noiseerrpocs,noisefxspf,noiseerrfxspf Figure 22. Reconstructed result (a) and interpolation error (b) using the 2D seislet POCS, Reconstructed result (c) and interpolation error (d) using the 2D Fourier POCS, reconstructed result (e) and interpolation error (f) using the 2D - SPF.


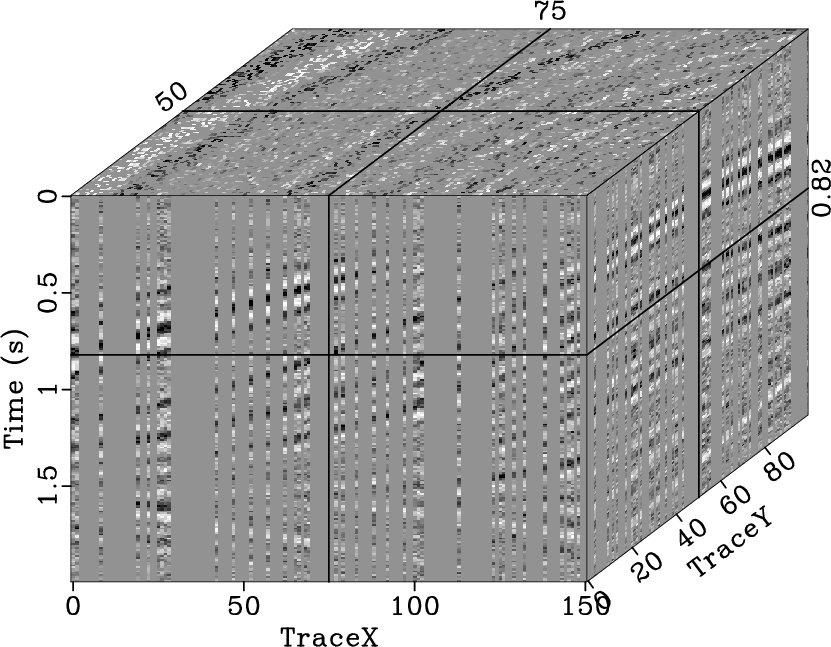
noiseqdome,noisegapqd Figure 23. Synthetic 3D model with random noise (a), model with $70\%$ of the data traces randomly removed (b).


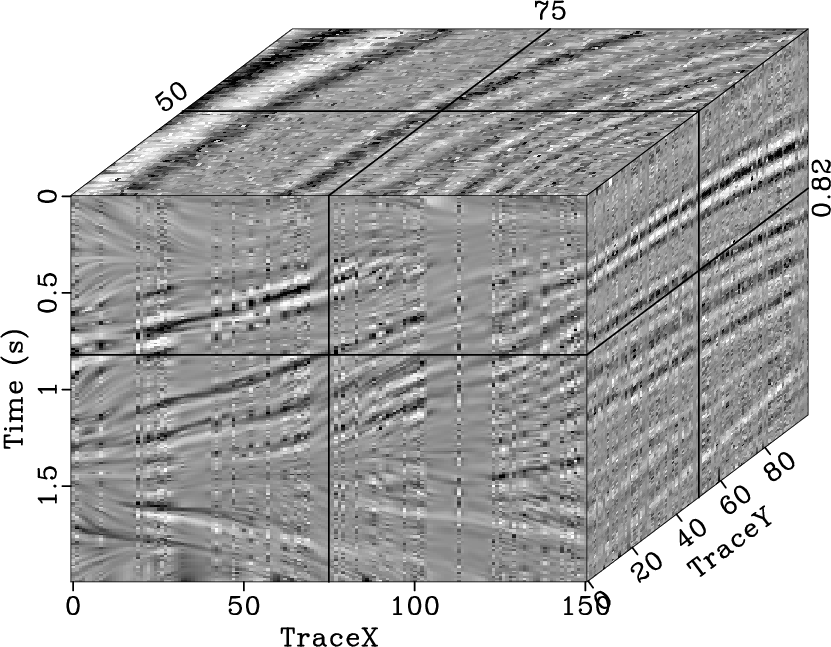
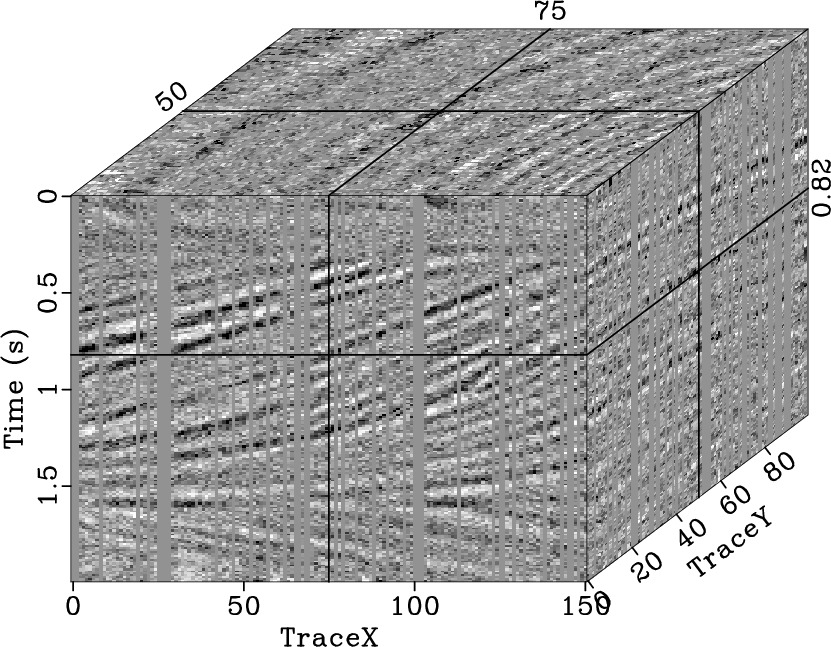
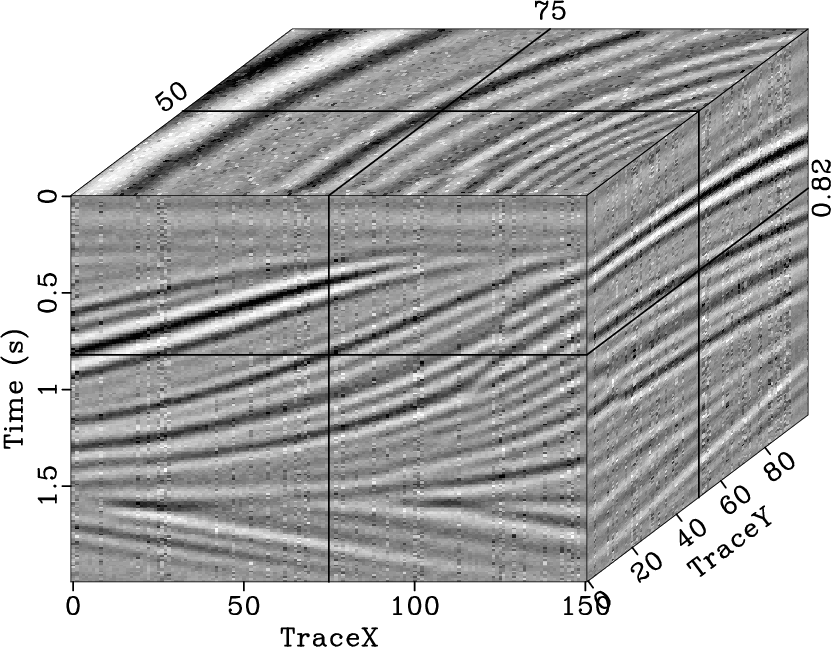
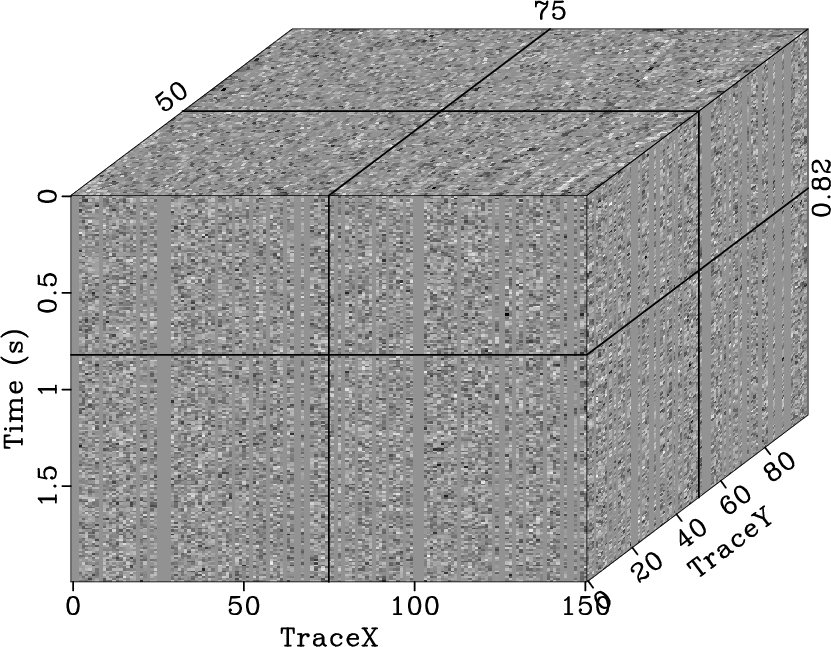
noisestpocsqd,noiseerrstpocsqd,noisepocsqd,noiseerrpocsqd,noisespfqd,noiseerrspfqd Figure 24. Reconstructed result (a) and interpolation error (b) using the 2D seislet POCS, reconstructed result (c) and interpolation error (d) using the 3D Fourier POCS, reconstructed result (e) and interpolation error (f) using the 3D - - SPF.

Next: Conclusion Up: Zheng et al.: Interpolation Previous: 3D data interpolation using

2022-04-15