Nonstationary signal and random noise separation

Next: Nonstationary signal and ground-roll Up: Data examples Previous: Data examples

Nonstationary signal and random noise separation

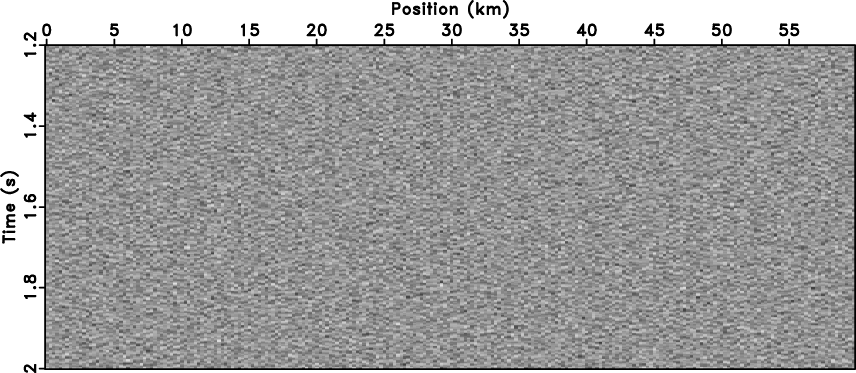
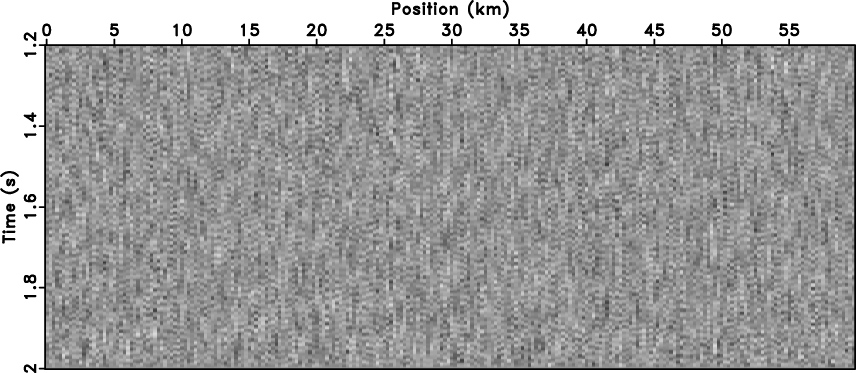
We started with a synthetic model (figure 1a) containing a curve event with varying slope. Figure 1b is the model data with the white Gaussian noise added. The F-K spectra (figure 2) show that the strong random noise severely affects the curve model. For comparison, we first used FXDECON, a standard industry method, to separate the signal from the noisy data. We designed the FXDECON with four-sample (space) filter size and ten-sample (space) sliding window. Although the FXDECON method results in a highest SNR (Table 1), it still fails to deal with strong random noise. The strong random noise has been suppressed in the estimated signal section (figure 3a), but a large part of signal is also destroyed and leaves the estimated noise section (figure 3b). Due to the strong energy of the random noise, the high SNR is caused by the suppression of both noise and signal. To demonstrate the effectiveness of the proposed nonstationary APEF, we separated the random noise using the pattern-based method (equation 7) with the stationary PEF in the t-x domain. The filter size of data pattern (PEF) D is selected with 11 (time) $\times$ 4 (space), noise pattern (PEF) N is 5 (time) $\times$ 1 (space) coefficients. Figure 3c shows that the stationary approach fails in separating the random noise in the estimated signal section as the stationary PEF is hard to characterize the nonstationary data pattern. Meanwhile, some energy appears from the signal in the estimated noise section (figure 3d). Figure 3e shows the denoised result of the curvelet transform with percentage threshold; this method effectively suppresses the random noise in the range from about 30 to 100 Hz (figure 4c), but it generates striped noise interference that affects the quality of the synthetic model. For the proposed method, we configured the APEF with the same filter size as that of the stationary PEF. The smoothing radii in the time and space directions for data pattern (APEF) $\mathbf{D}$ is selected to be 30 and 15 samples, respectively. And the noise pattern (APEF) $\mathbf{N}$ has a 300-sample (time) $\times$ 1-sample (space) smoothing radius. Figure 3g contains a part of the low-level noise, while the curve event has been recovered. The proposed method shows better signal protection ability, and obtains the denoised result at a high SNR level (Table 1). Here the SNR is calculated by equation 13:

$\displaystyle SNR = 10 \log_{10} ( \frac{\Vert \mathbf{s} \Vert _{2}^{2}} {\Vert \mathbf{s} - \mathbf{\bar{s}} \Vert _{2}^{2}})$

(13)

where $\mathbf{s}$ denotes effective signal, $\mathbf{\bar{s}}$ denotes denoised result. In the F-K spectra (figure 4), the energy of the curve event can be identified only in the denoised results using the curvelet transform and proposed method.

Synthetic model

FXDECON

Stationary PEF

Curvelet transform

	The
	proposed
	method

SNR

-9.432

-3.957

-5.176

-5.414

-5.029

Table 1. Comparison of the SNR of the random noise attenuation results


cm-data,cm-noiz Figure 1. (a) Clean data with curve event and (b) data with random noise.


cm-fkdata,cm-fknoiz Figure 2. (a) F-K spectra of clean data and (b) noisy data.


cm-fx,cm-fxnoiz,cm-pef,cm-pefnoiz,cm-ct,cm-ctnoiz,cm-apef,cm-apefnoiz Figure 3. (a) Estimated signal and (b) random noise by the FXDECON. (c) Estimated signal and (d) random noise by the pattern-based method with the stationary PEF. (e) Estimated signal and (f) random noise by the curvelet transform. (g) Estimated signal and (h) random noise by the proposed method.


cm-fkfx,cm-fkpef,cm-fkct,cm-fkapef Figure 4. (a)F-K spectrum of the denoised result using the FXDECON. (b) F-K spectrum of the denoised result using the pattern-based method with the stationary PEF. (c) F-K spectrum of the denoised result using the curvelet transform. (d) F-K spectrum of the denoised result using the proposed method.

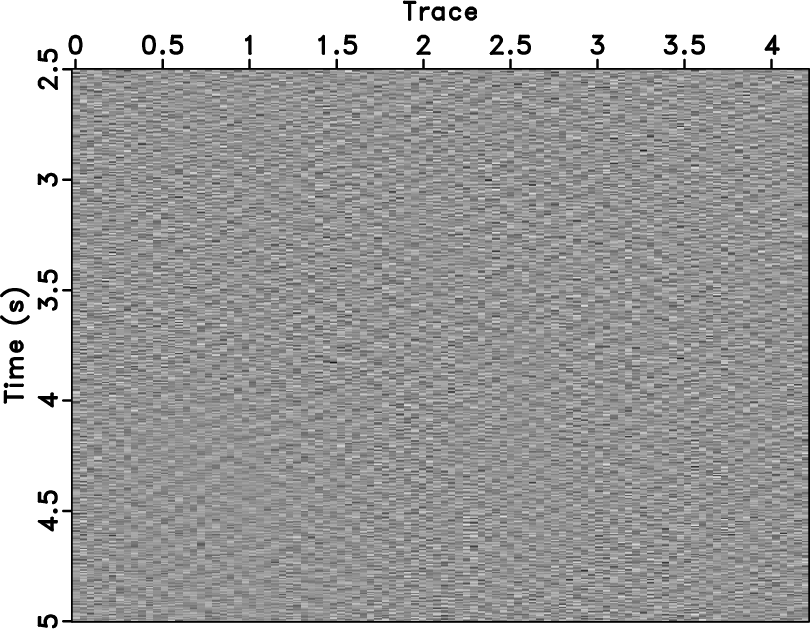
Figure 5 shows a poststack section, where the random noise influences the continuity of the reflection events. The data includes dipping beds and a fault. The main challenge in this example is that the random noise displays the nonstationary energy distribution. Figure 6 shows the separation results by using FXDECON, the filter size has eight sample (space) coefficients for each data sample and a 30-sample (space) sliding window for handling the variation of the signals. The FXDECON method fails in separating the nonstationary signal and random noise; weak energy random noise is still present in the signal section (figure 6a) and part of the signal leaks into the noise section (figure 6b). 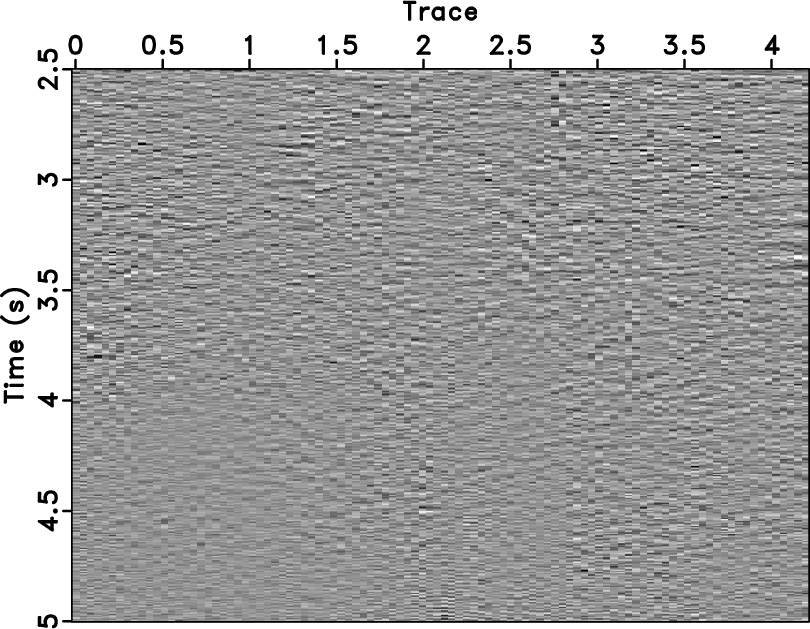By using the pattern-based method with the stationary PEF, we got the denoised result in figure 7. The data pattern (PEF) $\mathbf{D}$ is selected with 11 (time) $\times$ 4 sample (space) coefficients, noise pattern (PEF) $\mathbf{D}$ has 9 (time) $\times$ 1 sample (space) coefficients. In figure 7, the denoised result contains some high frequency noise, and part of the signal is removed. As shown in figure 10b, the energy of effective signal at about 18 Hz is partially filtered out. In the denoised result of curvelet transform with percentage threshold (figure 8), the random noise causes a stronger smearing of the events. Then we deal with the post- stack section by using the proposed method. The data APEF $\mathbf{D}$ has 9 (time) $\times$ 4 sample (space) coefficients for each sample and the smoothing radius is selected to be 60 (time) and 20 samples (space). The noise APEF $\mathbf{N}$ is designed as a 9 (time) $\times$ 1 sample (space) coefficients with a 60 (time) $\times$ 1 sample (space) smoothing radius. The estimated signal section displays that the continuity of the reflection layers with better smoothness is enhanced, and the fault is well preserved (figure 9a). The energy of the events and fault hardly leak into the noise section (figure 9b). The F-K spectrum in figure 10d is cleaner and the effective signal energy is concentrated. It indicates that the proposed method has a better capability for noise suppression and signal protection than other methods.


nmo-data,nmo-fkdata Figure 5. (a) Poststack section with random noise and (b) the corresponding F-K spectrum.


nmo-fx,nmo-fxnoiz Figure 6. Random noise separation results of the poststack section using the FXDECON. (a) Section of estimated signal and (b) section of separated random noise.


nmo-hpef,nmo-hpefnoiz Figure 7. Random noise separation results of the poststack section using the pattern-based method with the stationary PEF. (a) Section of estimated signal and (b) section of separated random noise.


nmo-ct,nmo-ctnoiz Figure 8. Random noise separation results of the poststack section using the curvelet transform. (a) Section of estimated signal and (b) section of separated random noise.


nmo-apef,nmo-apefnoiz Figure 9. Random noise separation results of the poststack section using the proposed method. (a) Section of estimated signal and (b) section of separated random noise.


nmo-fkfx,nmo-fkhpef,nmo-fkct,nmo-fkapef Figure 10. (a)F-K spectrum of the denoised result using the FXDECON. (b) F-K spectrum of the denoised result using the pattern-based method with the stationary PEF. (c) F-K spectrum of the denoised result using the curvelet transform. (d) F-K spectrum of the denoised result using the proposed method.

Next: Nonstationary signal and ground-roll Up: Data examples Previous: Data examples

2022-04-11