Homework 2

Data attributes and convolution

You can either write your answers to theoretical questions on paper or edit them in the file hw2/paper.tex. Please show all the mathematical derivations that you perform.

1. The varimax attribute is defined as
   

   $$\phi[\mathbf{a}] = \frac{\displaystyle N\,\sum\limits_{n=1... ...n^4}{\displaystyle \left(\sum\limits_{n=1}^{N} a_n^2\right)^2}$$ (1)

   
   

   Suppose that the data vector 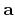$\mathbf{a}$ contains random noise: the data values 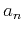$a_n$ are independent and identically distributed with a zero-mean Gaussian distribution: $E[a_n]=0$, $E[a_n^2]=\sigma^2$, $E[a_n^4]=3\,\sigma^4$. Find the mathematical expectation of $\phi[\mathbf{a}]$.

2. Consider the parabolic filter 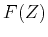$F(Z)$ defines as
   

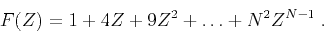   $$F(Z) = 1 + 4 Z + 9 Z^2 + \ldots + N^2 Z^{N-1}\;.$$ (2)

   
   
   1. Show that this filter can be implemented using recursive filtering (polynomial division).
   2. What is the advantage of recursive filtering? Does it depend on $N$?

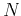3. Show that, using the helix transform and imposing helical boundary conditions, it is possible to compute a 2-D digital Fourier transform using 1-D FFT program. Assuming the input data is of size 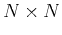$N \times N$, would this approach have any computational advantages?

Homework 2