Nonstationarity: patching

Dip rejecting known-velocity waves

Consider the two-dimensional filter

$$\begin{array}{rrr} \ & +1 & \ \\ -1 & 0 & -1 \\ \ & +1 & \ \end{array}$$ (3)

When this this filter is applied to a field profile with 4 ms time sampling and 6 m trace spacing, it should perfectly extinguish 1.5 km/s water-velocity noises. Likewise, the filter

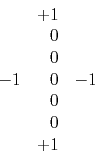$$\begin{array}{rrr} \ & +1 & \ \\ \ & 0 & \ \\ \ & 0 & \ \\ -1 & 0 & -1 \\ \ & 0 & \ \\ \ & 0 & \ \\ \ & +1 & \ \end{array}$$ (4)

should perfectly extinguish water noise when the trace spacing is 18 m. Such noise is, of course, spatially aliased for all temporal frequencies above 1/3 of Nyquist, but that does not matter. The filter extinguishes them perfectly anyway. Inevitably, the filter cannot both extinguish the noise and leave the signal untouched where the alias of one is equal to the other. So we expect the signal to be altered where it matches aliased noise. This simple filter does worse than that. On horizontal layers, for example, signal wavelets become filtered by $(1,0,0,-2,0,0,1)$ . If the noise is overwhelming, this signal distortion is a small price to pay for eliminating it. If the noise is tiny, however, the distortion is unforgivable. In the real world, data-adaptive deconvolution is usually a good compromise.

The two-dimensional deconvolutions filters we explore here look like this:

$$\begin{array}{ccccccccc} x& x& x& x& x& x& x& x& x \\ x& x& x... ....& .& .& .& .& .& .& . \\ .& .& .& .& 1& .& .& .& . \end{array}$$ (5)

where each $.$ denotes a zero and each $x$ denotes a (different) adjustable filter coefficient that is chosen to minimize the power out.

You can easily imagine variations on this shape, such as a diamond instead of a triangle. I invite you to experiment with the various shapes that suggest themselves.

Nonstationarity: patching