 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: The plane-wave destructor
Up: UNIVARIATE LEAST SQUARES
Previous: Imaging
This book defines many geophysical estimation applications.
Many applications amount to fitting two goals.
The first goal is a data-fitting goal,
the goal that the model should imply some observed data.
The second goal is that the model be not too big nor too wiggly.
We state these goals as two residuals, each of which is ideally zero.
A very simple data fitting goal would be that
the model  equals the data
equals the data  ,
thus the difference should vanish, say
,
thus the difference should vanish, say
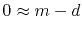 .
A more interesting goal is that the model should match the data
especially at high frequencies but not necessarily at low frequencies.
.
A more interesting goal is that the model should match the data
especially at high frequencies but not necessarily at low frequencies.
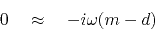 |
(9) |
A danger of this goal is that the model could have a zero-frequency component
of infinite magnitude as well as large amplitudes for low frequencies.
To suppress such bad behavior we need the second goal, a model residual
to be minimized. We need a small number  .
The model goal is:
.
The model goal is:
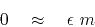 |
(10) |
To see the consequence of these two goals,
we add the squares of the residuals:
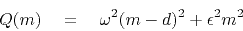 |
(11) |
and then, we minimize 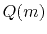 by setting its derivative to zero:
by setting its derivative to zero:
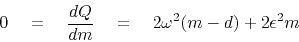 |
(12) |
or
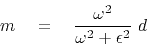 |
(13) |
Let us rename  to give it physical units of frequency
to give it physical units of frequency
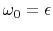 .
Our expression says
says
.
Our expression says
says  matches
matches  except for low frequencies
except for low frequencies
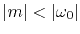 where it tends to zero.
Now we recognize we have a low-cut filter with
``cut-off frequency''
where it tends to zero.
Now we recognize we have a low-cut filter with
``cut-off frequency'' 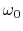 .
.
 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: The plane-wave destructor
Up: UNIVARIATE LEAST SQUARES
Previous: Imaging
2014-12-01
![]() equals the data
equals the data ![]() ,
thus the difference should vanish, say
,
thus the difference should vanish, say
![]() .
A more interesting goal is that the model should match the data
especially at high frequencies but not necessarily at low frequencies.
.
A more interesting goal is that the model should match the data
especially at high frequencies but not necessarily at low frequencies.