 |
 |
 |
 | Plane waves in three dimensions |  |
![[pdf]](icons/pdf.png) |
Next: My view of the
Up: THE LEVELER: A VOLUME
Previous: THE LEVELER: A VOLUME
The problem I found with
finite-difference representations of differential operators
is that they are susceptible to spatial aliasing.
Even before they encounter spatial aliasing,
they are susceptible to accuracy problems known
in finite-difference wave propagation as ``frequency dispersion.''
The aliasing problem can be avoided by the use of spatial prediction operators
such as
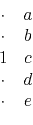 |
(1) |
where the vertical axis is time;
the horizontal axis is space; and
the ``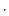 ''s are zeros.
Another possibility is the 2-D whitening filter
''s are zeros.
Another possibility is the 2-D whitening filter
 |
(2) |
Imagine all the coefficients vanished but 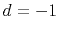 and the given 1.
Such filters would annihilate the appropriately sloping plane wave.
Slopes that are not exact integers are also approximately extinguishable,
because the adjustable filter coefficients can interpolate in time.
Filters like (2)
do the operation
and the given 1.
Such filters would annihilate the appropriately sloping plane wave.
Slopes that are not exact integers are also approximately extinguishable,
because the adjustable filter coefficients can interpolate in time.
Filters like (2)
do the operation
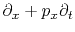 ,
which is a component of the gradient in the plane of the wavefront,
and
they include a temporal deconvolution aspect
and a spatial coherency aspect.
My experience shows that the operators (1) and
(2)
behave significantly differently in practice,
and I am not prepared to fully explain the difference,
but it seems to be similar to the gapping of one-dimensional filters.
,
which is a component of the gradient in the plane of the wavefront,
and
they include a temporal deconvolution aspect
and a spatial coherency aspect.
My experience shows that the operators (1) and
(2)
behave significantly differently in practice,
and I am not prepared to fully explain the difference,
but it seems to be similar to the gapping of one-dimensional filters.
You might find it alarming
that your teacher is not fully prepared
to explain the difference between a volume and two planes,
but please remember that we are talking about
the factorization of the volumetric spectrum.
Spectral matrices are well known to have structure,
but books on theory typically handle them as simply
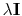 .
Anyway, wherever you see an
.
Anyway, wherever you see an 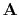 in a three-dimensional context,
you may wonder whether it should be interpreted as a cubic filter
that takes one volume to another,
or as two planar filters
that take one volume to two volumes
as shown in Figure 2.
in a three-dimensional context,
you may wonder whether it should be interpreted as a cubic filter
that takes one volume to another,
or as two planar filters
that take one volume to two volumes
as shown in Figure 2.
rayab3Doper
Figure 2.
An inline 2-D PEF and a crossline 2-D PEF
both applied throughout the volume.
To find each filter,
minimize each output power independently.
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[xfig]](icons/xfig.png)
|
|---|
 |
 |
 |
 | Plane waves in three dimensions |  |
![[pdf]](icons/pdf.png) |
Next: My view of the
Up: THE LEVELER: A VOLUME
Previous: THE LEVELER: A VOLUME
2013-07-27
![]() .
Anyway, wherever you see an
.
Anyway, wherever you see an ![]() in a three-dimensional context,
you may wonder whether it should be interpreted as a cubic filter
that takes one volume to another,
or as two planar filters
that take one volume to two volumes
as shown in Figure 2.
in a three-dimensional context,
you may wonder whether it should be interpreted as a cubic filter
that takes one volume to another,
or as two planar filters
that take one volume to two volumes
as shown in Figure 2.
