 |
 |
 |
 | Time-shift imaging condition for converted waves |  |
![[pdf]](icons/pdf.png) |
Next: Angle decomposition
Up: Imaging condition
Previous: Conventional imaging condition
We can formulate a more general imaging condition
based on cross-correlation of the source and receiver
wavefields after shifting in both time and space.
Mathematically, we can represent this process by the relations
Here,
![${ \bf h}= \left[ h_x,h_y,h_z \right]$](img26.png) is a vector describing the local
source-receiver separation in the image space, and
is a vector describing the local
source-receiver separation in the image space, and
 is a time-shift between the source
and receiver wavefields prior to imaging.
In this imaging condition we do not assume that the
source and receiver wavefields maximize image strength
at the zero-lag of the space-time cross-correlation.
Instead, we probe wavefield similitude at other lags using
both shifting in space and time.
is a time-shift between the source
and receiver wavefields prior to imaging.
In this imaging condition we do not assume that the
source and receiver wavefields maximize image strength
at the zero-lag of the space-time cross-correlation.
Instead, we probe wavefield similitude at other lags using
both shifting in space and time.
This imaging condition can be implemented in the
Fourier domain using the expression
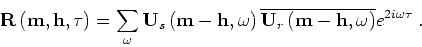 |
(6) |
Special cases of this imaging condition correspond to
purely space-shift 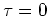 , when the imaging condition reduces to
(Sava and Fomel, 2005a)
, when the imaging condition reduces to
(Sava and Fomel, 2005a)
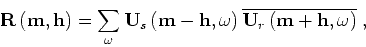 |
(7) |
or purely time-shift 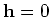 , when the imaging condition reduces to
(Sava and Fomel, 2006)
, when the imaging condition reduces to
(Sava and Fomel, 2006)
 |
(8) |
The imaging procedures described in this section produce
images that can be used for angle decomposition
of reflectivity at every image location, thus making this
imaging procedure useful for MVA or AVA.
The imaging conditions presented in this section make no assumption
on the nature of the source and receiver wavefields
We can reconstruct those two wavefields using any type of
extrapolation, or using different velocity models for extrapolation of
the source and receiver wavefields.
In the following section, we discuss angle-decomposition based on the
images obtained by conditions described in the current section.
For angle decomposition, we cannot ignore anymore the physical nature
of the two wavefields we are comparing, and we need to specify
what type of wave (P or S) do the various wavefields correspond to.
For the following analysis, we will assume that source wavefields
correspond to incident P waves, and receiver wavefields correspond to
reflected S waves.


|
|---|
experimentC,vecC
Figure 1. (a) Synthetic PS reflection experiment, and
(b) Geometric relations between ray vectors at an image point.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[xfig]](icons/xfig.png) ![[xfig]](icons/xfig.png)
|
|---|
 |
 |
 |
 | Time-shift imaging condition for converted waves |  |
![[pdf]](icons/pdf.png) |
Next: Angle decomposition
Up: Imaging condition
Previous: Conventional imaging condition
2008-11-26

