 |
 |
 |
 | Elastic wave-mode separation for TTI media |  |
![[pdf]](icons/pdf.png) |
Next: Marmousi II model
Up: Examples
Previous: Examples
Consider the 2D fold model shown in
Figure 9.
Panels 9(a)-fig:fold-aoppos show  ,
,  ,
density, parameters
,
density, parameters  ,
,  , and the local tilts
, and the local tilts  of
the model, respectively. The symmetry axis is orthogonal to the
reflectors throughout the model.
Figure 10
illustrates the separators obtained at different locations in the
model and defined by the intersections of
of
the model, respectively. The symmetry axis is orthogonal to the
reflectors throughout the model.
Figure 10
illustrates the separators obtained at different locations in the
model and defined by the intersections of  coordinates
coordinates
 km and
km and  coordinates
coordinates
 km, shown by the dots
in Figure 9(f). Since the operators correspond to different
combinations of the
km, shown by the dots
in Figure 9(f). Since the operators correspond to different
combinations of the
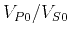 ratio and parameters
ratio and parameters  ,
,
 , and tilt angle
, and tilt angle  , they have different forms. However, the
orientation of the operators conform to the corresponding tilts at the
locations shown by the dots in Figure 9(f). For complex models, the
symmetry axes vary spatially, which makes it difficult to rotate the
wavefields to the local symmetry axis directions. Consequently, the
elastic wavefields are reconstructed in untilted Cartesian
coordinates, and when separating wave-modes, I use operators
constructed in conventional Cartesian coordinates. To illustrate the
relationship between the operators and the local tilts, the filters
in Figure 10 are projected onto the local symmetry axes and the
orthogonal directions at the filter location. As shown
in Figure 4, the rotated filters (Figure
, they have different forms. However, the
orientation of the operators conform to the corresponding tilts at the
locations shown by the dots in Figure 9(f). For complex models, the
symmetry axes vary spatially, which makes it difficult to rotate the
wavefields to the local symmetry axis directions. Consequently, the
elastic wavefields are reconstructed in untilted Cartesian
coordinates, and when separating wave-modes, I use operators
constructed in conventional Cartesian coordinates. To illustrate the
relationship between the operators and the local tilts, the filters
in Figure 10 are projected onto the local symmetry axes and the
orthogonal directions at the filter location. As shown
in Figure 4, the rotated filters (Figure ![[*]](icons/crossref.png) ) show
a clearer relation with the tilt angle, while the non-rotated filters
(Figure
) show
a clearer relation with the tilt angle, while the non-rotated filters
(Figure ![[*]](icons/crossref.png) ), which are used in the wave-mode separation, do not
show a clear relation with the tilt angle.
), which are used in the wave-mode separation, do not
show a clear relation with the tilt angle.
Figure 11(a) shows the vertical and horizontal components of one snapshot
of the simulated elastic anisotropic wavefield; Figure 11(b) shows the
separation into P- and S-modes using divergence and curl
operators; Figure 11(c) shows the separation into qP and qS
modes using VTI filters, i.e., assuming zero tilt throughout the
model; and Figure 11(d) shows the separation obtained with the TTI
operators constructed using the local medium parameters with correct
tilts. The isotropic separation shown in Figure 11(b) is incomplete; for
example, at 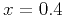 km and
km and  km, and at
km, and at 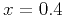 km and
km and  km, residuals for direct P and S arrivals are visible in the qP
and qS panels, respectively. A comparison of Figures 11(c)
and fig:pA indicates that the spatially-varying derivative operators
with correct tilts successfully separate the elastic wavefields into
qP and qS modes, while the VTI operators only work in the
part of the model that is locally VTI.
km, residuals for direct P and S arrivals are visible in the qP
and qS panels, respectively. A comparison of Figures 11(c)
and fig:pA indicates that the spatially-varying derivative operators
with correct tilts successfully separate the elastic wavefields into
qP and qS modes, while the VTI operators only work in the
part of the model that is locally VTI.






|
|---|
vp,vs,ro,epsilon,delta,aoppos
Figure 9. A fold model with parameters (a)  , (b)
, (b)  , (c) density,
(d)
, (c) density,
(d)  , (e)
, (e)  , and (f) tilt angle
, and (f) tilt angle  . The dots in
panel (f) correspond to the locations of the anisotropic operators
shown in Figure 10.
. The dots in
panel (f) correspond to the locations of the anisotropic operators
shown in Figure 10.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|

|
|---|
rop
Figure 10. The TTI wave-mode separation filters projected to
local symmetry axes and their orthogonal directions. Here, I use
 in equation 12 to taper the polarization vector
components before the Fourier transform. The filters correspond to the
intersections of
in equation 12 to taper the polarization vector
components before the Fourier transform. The filters correspond to the
intersections of  ,
,  ,
,  km and
km and  ,
,  ,
,
 km for the model shown
in Figure 9. The locations of these
operators are also shown by the dots in Figure 9(f).
km for the model shown
in Figure 9. The locations of these
operators are also shown by the dots in Figure 9(f).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|




|
|---|
uA,pI,pV,pA
Figure 11. (a) A snapshot of the anisotropic wavefield simulated with a vertical
point displacement source at 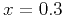 km and
km and  km for the model
shown in Figure 9. Panels (b) to (d)
are the anisotropic qP and qS modes separated using
isotropic, VTI, and TTI separators, respectively. The separation is
incomplete in panels (b) and (c) where the model is strongly
anisotropic and where the model tilt is large, respectively. Panel (d)
shows the best separation among all.
km for the model
shown in Figure 9. Panels (b) to (d)
are the anisotropic qP and qS modes separated using
isotropic, VTI, and TTI separators, respectively. The separation is
incomplete in panels (b) and (c) where the model is strongly
anisotropic and where the model tilt is large, respectively. Panel (d)
shows the best separation among all.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Elastic wave-mode separation for TTI media |  |
![[pdf]](icons/pdf.png) |
Next: Marmousi II model
Up: Examples
Previous: Examples
2013-08-29
![]() km and
km and ![]() km, and at
km, and at ![]() km and
km and ![]() km, residuals for direct P and S arrivals are visible in the qP
and qS panels, respectively. A comparison of Figures 11(c)
and fig:pA indicates that the spatially-varying derivative operators
with correct tilts successfully separate the elastic wavefields into
qP and qS modes, while the VTI operators only work in the
part of the model that is locally VTI.
km, residuals for direct P and S arrivals are visible in the qP
and qS panels, respectively. A comparison of Figures 11(c)
and fig:pA indicates that the spatially-varying derivative operators
with correct tilts successfully separate the elastic wavefields into
qP and qS modes, while the VTI operators only work in the
part of the model that is locally VTI.










