 |
 |
 |
 | Isotropic angle-domain elastic reverse-time migration |  |
![[pdf]](icons/pdf.png) |
Next: Vector wavefields
Up: Angle decomposition
Previous: Angle decomposition
For the case of imaging with the acoustic wave equation, the
reflection angle corresponding to incidence and reflection of P-wave
mode can be constructed after imaging, using mapping based on the
relation (Sava and Fomel, 2005)
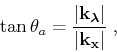 |
(11) |
where 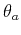 is the incidence angle, and
is the incidence angle, and
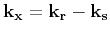 and
and
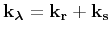 are defined using the source and
receiver wavenumbers,
are defined using the source and
receiver wavenumbers,
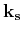 and
and
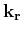 . The information
required for decomposition of the reconstructed wavefields as
a function of wavenumbers
. The information
required for decomposition of the reconstructed wavefields as
a function of wavenumbers
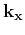 and
and
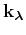 is readily
available in the images
is readily
available in the images
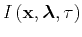 constructed by extended imaging
conditions equations
constructed by extended imaging
conditions equations ![[*]](icons/crossref.png) or
or ![[*]](icons/crossref.png) .
After angle decomposition, the image
.
After angle decomposition, the image
 represents a
mapping of the image
represents a
mapping of the image
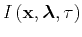 from offsets to angles. In other
words, all information for characterizing angle-dependent reflectivity
is already available in the image obtained by the extended imaging
conditions.
from offsets to angles. In other
words, all information for characterizing angle-dependent reflectivity
is already available in the image obtained by the extended imaging
conditions.
2013-08-29