 |
 |
 |
 | Moveout, velocity, and stacking |  |
![[pdf]](icons/pdf.png) |
Next: THE NORMAL MOVEOUT MAPPING
Up: INTERPOLATION AS A MATRIX
Previous: Looping over output space
We have thought of equation (4.1)
as a formula for finding 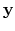 from
from 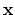 .
Now consider the opposite problem, finding
.
Now consider the opposite problem, finding 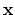 from
from 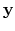 .
Begin by multiplying equation (4.2)
by the transpose matrix
to define a new quantity
.
Begin by multiplying equation (4.2)
by the transpose matrix
to define a new quantity 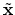 :
:
![\begin{displaymath}
\left[
\begin{array}{c}
\tilde x_1 \\
\tilde x_2 \\
...
... y_2 \\
y_3 \\
y_4 \\
y_5 \\
y_6
\end{array} \right]
\end{displaymath}](img12.png) |
(3) |
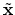 is not the same as
is not the same as 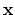 ,
but these two vectors have the same dimensionality
and in many applications
it may happen that
,
but these two vectors have the same dimensionality
and in many applications
it may happen that
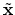 is a good approximation to
is a good approximation to 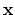 .
In general,
.
In general,
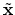 may be called an ``image'' of
may be called an ``image'' of 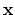 .
Finding the image is the first step of finding
.
Finding the image is the first step of finding 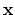 itself.
Formally, the problem is
itself.
Formally, the problem is
 |
(4) |
And the formal solution to the problem is
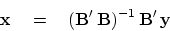 |
(5) |
Formally, we verify this solution by substituting
(4.4) into
(4.5).
 |
(6) |
In applications,
the possible nonexistence of an inverse for the matrix
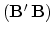 is always a topic for discussion.
For now we simply examine this matrix for the interpolation problem.
We see that it is diagonal:
is always a topic for discussion.
For now we simply examine this matrix for the interpolation problem.
We see that it is diagonal:
![\begin{displaymath}
\bold B' \bold B
\eq
\left[
\begin{array}{ccccccc}
1 ...
... \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 2
\end{array} \right] \;
\end{displaymath}](img16.png) |
(7) |
So,
 ; but
; but
 .
To recover the original data,
we need to divide
.
To recover the original data,
we need to divide  by the diagonal matrix
by the diagonal matrix
 .
Thus, matrix inversion is easy here.
.
Thus, matrix inversion is easy here.
Equation
(4.5)
has an illustrious reputation, which
arises in the context of ``least squares.''
Least squares
is a general method for solving sets of equations
that have more equations than unknowns.
Recovering 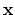 from
from 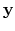 using equation
(4.5)
presumes the existence of the inverse of
using equation
(4.5)
presumes the existence of the inverse of
 .
As you might expect, this matrix is nonsingular when
.
As you might expect, this matrix is nonsingular when  stretches the data,
because then a few data values are distributed
among a greater number of locations.
Where the transformation squeezes the data,
stretches the data,
because then a few data values are distributed
among a greater number of locations.
Where the transformation squeezes the data,
 must become singular,
since returning
uniquely to the uncompressed condition is impossible.
must become singular,
since returning
uniquely to the uncompressed condition is impossible.
We can now understand why an adjoint operator is often an
approximate inverse.
This equivalency happens in proportion to the nearness of the matrix
 to an identity matrix.
The interpolation example we have just examined is one in which
to an identity matrix.
The interpolation example we have just examined is one in which
 differs from an identity matrix merely by a scaling.
differs from an identity matrix merely by a scaling.
 |
 |
 |
 | Moveout, velocity, and stacking |  |
![[pdf]](icons/pdf.png) |
Next: THE NORMAL MOVEOUT MAPPING
Up: INTERPOLATION AS A MATRIX
Previous: Looping over output space
2009-03-16
![\begin{displaymath}
\left[
\begin{array}{c}
\tilde x_1 \\
\tilde x_2 \\
...
... y_2 \\
y_3 \\
y_4 \\
y_5 \\
y_6
\end{array} \right]
\end{displaymath}](img12.png)
![\begin{displaymath}
\bold B' \bold B
\eq
\left[
\begin{array}{ccccccc}
1 ...
... \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 2
\end{array} \right] \;
\end{displaymath}](img16.png)
![]() from
from ![]() using equation
(4.5)
presumes the existence of the inverse of
using equation
(4.5)
presumes the existence of the inverse of
![]() .
As you might expect, this matrix is nonsingular when
.
As you might expect, this matrix is nonsingular when ![]() stretches the data,
because then a few data values are distributed
among a greater number of locations.
Where the transformation squeezes the data,
stretches the data,
because then a few data values are distributed
among a greater number of locations.
Where the transformation squeezes the data,
![]() must become singular,
since returning
uniquely to the uncompressed condition is impossible.
must become singular,
since returning
uniquely to the uncompressed condition is impossible.
![]() to an identity matrix.
The interpolation example we have just examined is one in which
to an identity matrix.
The interpolation example we have just examined is one in which
![]() differs from an identity matrix merely by a scaling.
differs from an identity matrix merely by a scaling.