Waves and Fourier sums

Basics of two-dimensional Fourier transform

Let us review some basic facts about two-dimensional Fourier transform. A two-dimensional function is represented in a computer as numerical values in a matrix, whereas a one-dimensional Fourier transform in a computer is an operation on a vector. A 2-D Fourier transform can be computed by a sequence of 1-D Fourier transforms. We can first transform each column vector of the matrix and then each row vector of the matrix. Alternately, we can first do the rows and later do the columns. This is diagrammed as follows:

$$\matrix{ p(t,\ x) & \smash{\mathop{\longleftrightarrow}} ... ... \smash{\mathop{\longleftrightarrow}} & P(\omega,\ k_x)\cr }$$

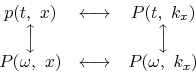
The diagram has the notational problem that we cannot maintain the usual convention of using a lower-case letter for the domain of physical space and an upper-case letter for the Fourier domain, because that convention cannot include the mixed objects $P(t , k_x )$ and $P ( \omega , x )$. Rather than invent some new notation, it seems best to let the reader rely on the context: the arguments of the function must help name the function.

An example of two-dimensional Fourier transforms on typical deep-ocean data is shown in Figure 4.

plane4
Figure 4. A deep-marine dataset $p(t , x)$ from Alaska (U.S. Geological Survey) and the real part of various Fourier transforms of it. Because of the long traveltime through the water, the time axis does not begin at $t=0$.

In the deep ocean, sediments are fine-grained and deposit slowly in flat, regular, horizontal beds. The lack of permeable rocks such as sandstone severely reduces the potential for petroleum production from the deep ocean. The fine-grained shales overlay irregular, igneous, basement rocks. In the plot of $P(t , k_x )$, the lateral continuity of the sediments is shown by the strong spectrum at low $k_x$. The igneous rocks show a $k_x$ spectrum extending to such large $k_x$ that the deep data may be somewhat spatially aliased (sampled too coarsely). The plot of $P ( \omega , x )$ shows that the data contains no low-frequency energy. The dip of the sea floor shows up in $( \omega , k_x )$-space as the energy crossing the origin at an angle.

Altogether, the two-dimensional Fourier transform of a collection of seismograms involves only twice as much computation as the one-dimensional Fourier transform of each seismogram. This is lucky. Let us write some equations to establish that the asserted procedure does indeed do a 2-D Fourier transform. Say first that any function of $x$ and $t$ may be expressed as a superposition of sinusoidal functions:

$$p(t , x) \ \ =\ \ \int \int \ e^{ -i \omega t + i k_x x } \ P( \omega , k_x ) \ d \omega \ d k_x$$ (26)

The double integration can be nested to show that the temporal transforms are done first (inside):

$$\begin{eqnarray*} p(t , x) \ \ &=&\ \ \int \ e^{ i \,k_x x } \ \left[ \int \ e^... ...k_x \\ \ \ &=&\ \ \int \ e^{ i \,k_x x } \ P(t , k_x ) \ dk_x \end{eqnarray*}$$

The quantity in brackets is a Fourier transform over $\omega$ done for each and every $k_x$. Alternately, the nesting could be done with the $k_x$-integral on the inside. That would imply rows first instead of columns (or vice versa). It is the separability of $\exp (-i \omega t \,+\, i\, k_x x )$ into a product of exponentials that makes the computation easy and cheap.

Waves and Fourier sums