A new paper is added to the collection of reproducible documents: One-step slope estimation for dealiased seismic data reconstruction via iterative seislet thresholding

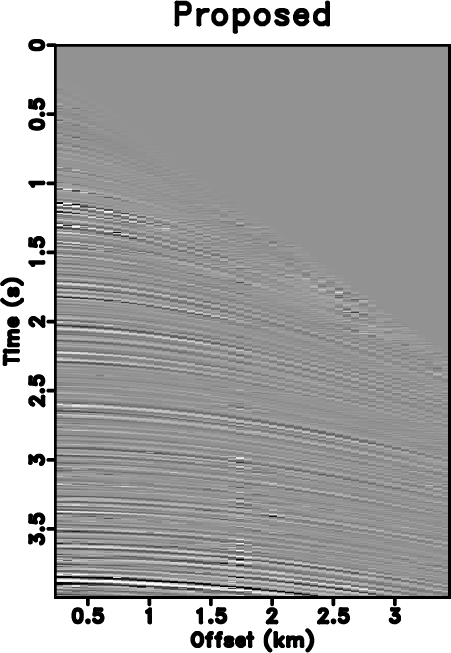
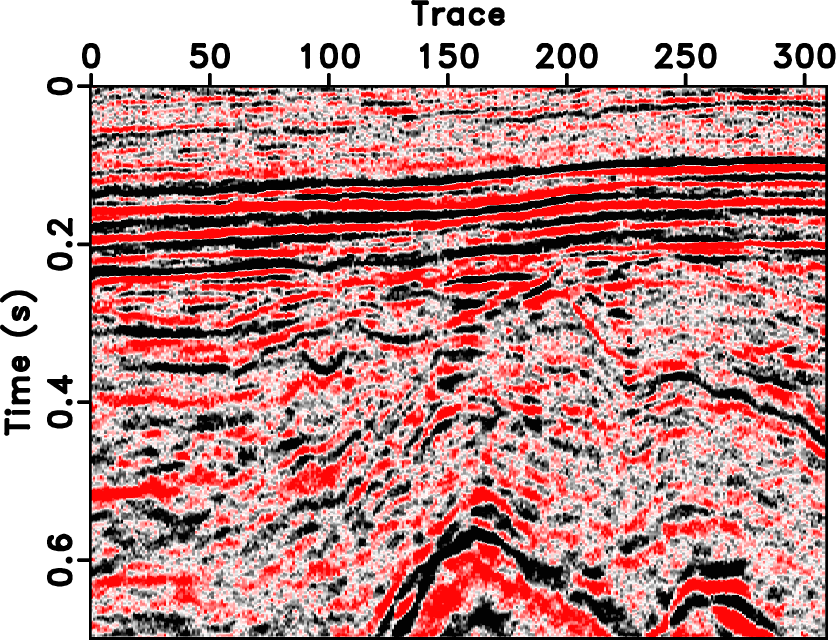
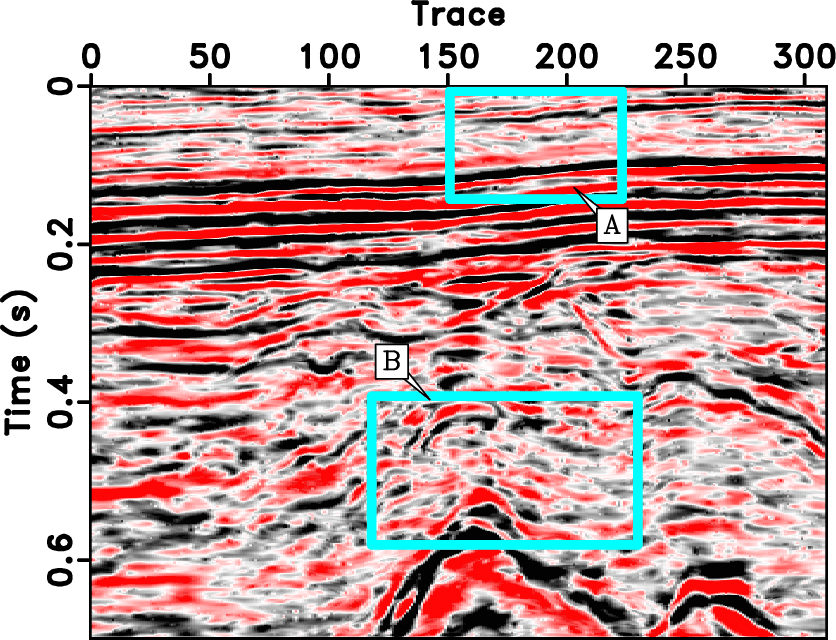
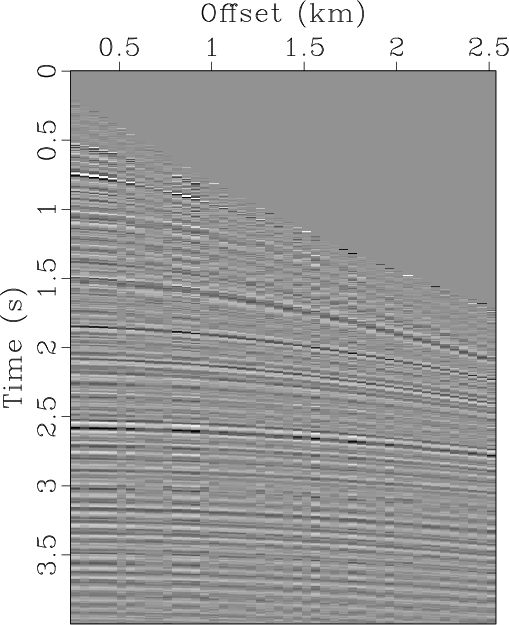
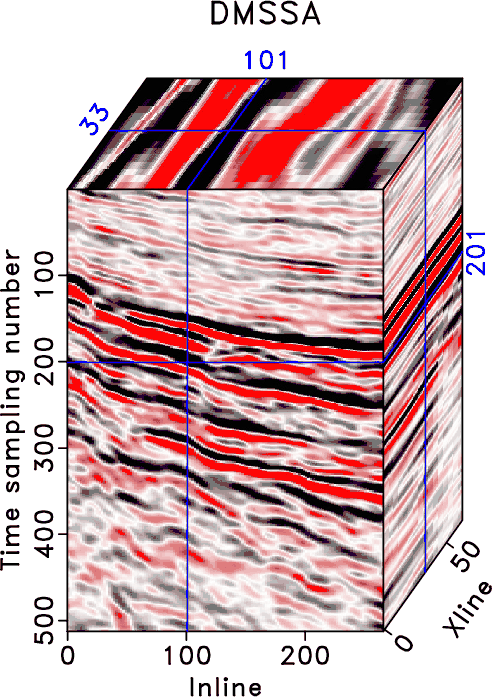
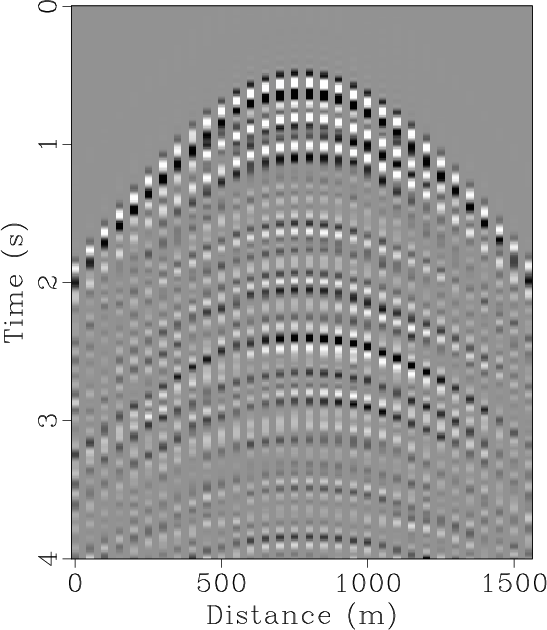
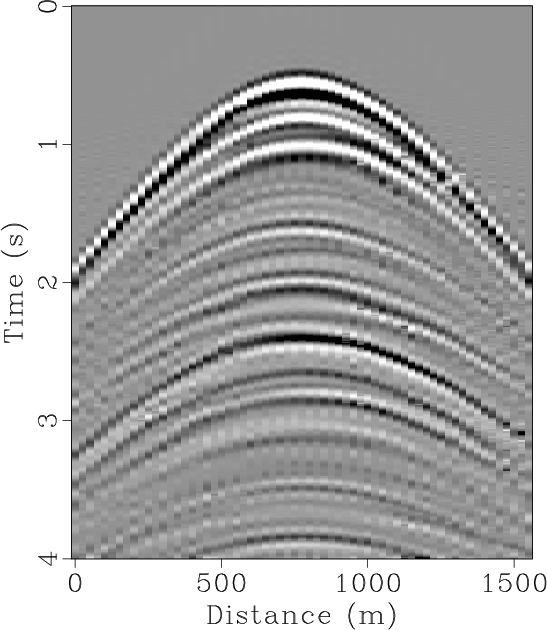
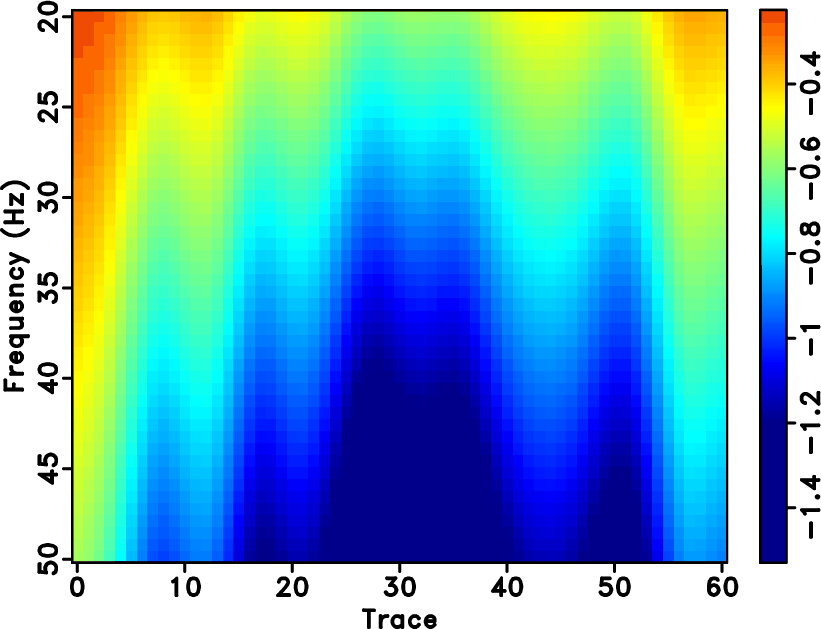
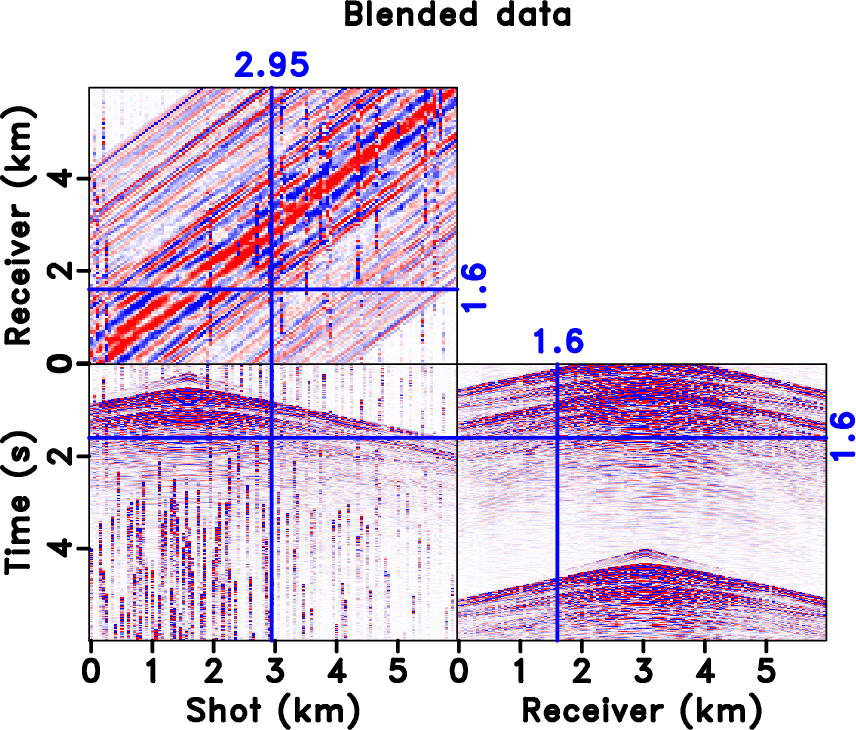
The seislet transform can be used to interpolate regularly under-sampled seismic data if an accurate local slope map can be obtained. The dealiasing capability of such method highly depends on the accuracy of the estimated local slope, which can be achieved by using the low-frequency components of the aliased seismic data in an iterative manner. Previous approaches to solving this problem have been limited to the unstable estimation of local slope via a large number of iterations. Here, we propose a new way to obtain the slope estimation. We first estimate the NMO velocity and then use a velocity-slope transformation to get the optimal local slope. The new method allows us to avoid the iterative slope estimation and can obtain an accurate slope field in one step. The one-step slope estimation can significantly accelerate the iterative seislet domain thresholding process and can also stabilize the iterative inversion. Both synthetic and field data examples are used to demonstrate the performance by using the proposed approach compared with alternative approaches.

A new paper is added to the collection of reproducible documents: Dip-separated structural filtering using seislet transform and adaptive empirical mode decomposition based dip filter

The seislet transform has been demonstrated to have a better compression performance for seismic data compared with other well-known sparsity promoting transforms, thus it can be used to remove random noise by simply applying a thresholding operator in the seislet domain. Since the seislet transform compresses the seismic data along the local structures, the seislet thresholding can be viewed as a simple structural filtering approach. Because of the dependence on a precise local slope estimation, the seislet transform usually suffers from low compression ratio and high reconstruction error for seismic profiles that have dip conflicts. In order to remove the limitation of seislet thresholding in dealing with conflicting-dip data, I propose a dip-separated filtering strategy. In this method, I first use an adaptive empirical mode decomposition based dip filter to separate the seismic data into several dip bands (5 or 6). Next, I apply seislet thresholding to each separated dip component to remove random noise. Then I combine all the denoised components to form the final denoised data. Compared with other dip filters, the empirical mode decomposition based dip filter is data-adaptive. Both complicated synthetic and field data examples show superior performance of my proposed approach than the traditional alternatives. The dip-separated structural filtering is not limited to seislet thresholding, and can also be extended to all those methods that require slope information.

A new paper is added to the collection of reproducible documents: Irregular seismic data reconstruction using a percentile-half-thresholding algorithm

In this paper, a percentile-half-thresholding approach is proposed in the transformed domain thresholding process for iterative shrinkage thresholding (IST). The percentile-thresholding strategy is more convenient for implementing than the constant-value, linear-decreasing, or exponential-decreasing thresholding because it’s data-driven. The novel half-thresholding strategy is inspired from the recent advancement in the researches on optimization using non-convex regularization. We summarize a general thresholding framework for IST and show that the only difference between half thresholding and the conventional soft or hard thresholding lays in the thresholding operator. Thus it’s straightforward to insert the existing percentile-thresholding strategy to the half-thresholding iterative framework. We use both synthetic and field data examples to compare the performances using soft thresholding or half thresholding with constant threshold or percentile threshold. Synthetic and field data show consistent results that apart from the threshold-setting convenience, the percentile thresholding also has the possibility for improving the recovery performance. Compared with soft thresholding, half thresholding tends to have a more precise reconstructed result.

A new paper is added to the collection of reproducible documents: Multiple reflections noise attenuation using adaptive randomized-order empirical mode decomposition

We propose a novel approach for removing multiple reflections noise based on an adaptive randomized-order empirical mode decomposition framework. We first flatten the primary reflections in common midpoint (CMP) gather using the automatically picked NMO velocities that correspond to the primary reflections and then randomly permutate all the traces. Next, we removed the spatially distributed random spikes that correspond to the multiple reflections using the EMD based smoothing approach that is implemented in the $f-x$ domain. The trace randomization approach can make the spatially coherent multiple reflections random along the space direction and can decrease the coherency of near-offset multiple reflections. The EMD based smoothing method is superior to median filter and prediction error filter in that it can help preserve the flattened signals better, without the need of exact flattening, and can preserve the amplitude variation much better. In addition, EMD is a fully adaptive algorithm and the parameterization for EMD based smoothing can be very convenient.

A new paper is added to the collection of reproducible documents: Damped multichannel singular spectrum analysis for 3D random noise attenuation

Multichannel singular spectrum analysis (MSSA) is an effective algorithm for random noise attenuation in seismic data, which decomposes the vector space of the Hankel matrix of the noisy signal into a signal subspace and a noise subspace by the truncated singular value decomposition (TSVD). However, this signal subspace actually still contains residual noise. We derived a new formula of low-rank reduction, which is more powerful in distinguishing between signal and noise compared with the traditional TSVD. By introducing a damping factor into the traditional MSSA for damping the singular values, we proposed a new algorithm for random noise attenuation. The proposed modified MSSA is named as the damped MSSA. The denoising performance is controlled by the damping factor and the proposed approach reverts to the traditional MSSA approach when the damping factor is sufficiently large. Application of the damped MSSA algorithm on synthetic and field seismic data demonstrates a superior performance compared with the conventional MSSA algorithm.

A new paper is added to the collection of reproducible documents: De-aliased seismic data interpolation using seislet transform with low-frequency constraint

Interpolating regularly missing traces in seismic data is thought to be much harder than interpolating irregularly missing seismic traces, because many sparsity-based approaches can not be used due to the strong aliasing noise in the sparse domain. We propose to use seislet transform to perform a sparsity-based approach to interpolate highly under-sampled seismic data based on the classic projection onto convex sets (POCS) framework. Many numerical tests show that the local slope is the main factor that will affect the sparsity and anti-aliasing ability of seislet transform. By low-pass filtering the under-sampled seismic data with a very low bound frequency, we can get a precise dip estimation, which will make seislet transform capable for interpolating the aliased seismic data. In order to prepare the optimum local slope during iterations, we update the slope field every several iterations. We also use a percentile thresholding approach to better control the reconstruction performance. Both synthetic and field examples show better performance using the proposed approach than the traditional prediction based and the $F-K$ POCS based approaches.

A new paper is added to the collection of reproducible documents: Multi-channel quality factor Q estimation

The estimation of quality factor, Q, plays an important role in many geophysical problems, including Q-compensated seismic imaging, geophysical interpretation, and fluid characterization. One of the most widely used approaches for estimating Q is the spectral ratio method (SRM). However, the spectral division in SRM may not be stable due to the spectral nulls. The shaping regularized inversion that treats the spectral division as a regularized least-squares inversion problem can help solve the spectral-nulls problem and make the spectral division stable. In the case of very noisy seismic data, the time-frequency maps can not be optimally obtained and thus the Q estimation performance will be strongly affected and unstable even with the regularized inversion method. We propose a multi-channel Q estimation approach that takes advantage of the multi-channel spatial coherence to constrain the inversion so that the estimated Q is spatially continuous. We use a set of synthetic and real data examples to demonstrate the performance of the multi-channel Q estimation method. Results show that the proposed method can obtain accurate and more importantly stable Q estimation result even in the case of strong random noise.

A new paper is added to the collection of reproducible documents: Deblending of simultaneous-source data using a structure-oriented space-varying median filter

In seismic data processing, the median filter is usually applied along the structural direction of seismic data in order to attenuate erratic or spike-like noise. The performance of a structure-oriented median filter highly depends on the accuracy of the estimated local slope from the noisy data. When local slope contains significant error, which is usually the case for noisy data, the structure-oriented median filter will still cause severe damages to useful energy. We propose a type of structure-oriented median filter that can effectively attenuate spike-like noise even when the local slope is not accurately estimated, which we call structure-oriented space-varying median filter. A structure-oriented space-varying median filter can adaptively squeeze and stretch the window length of the median filter when applied in the locally flattened dimension of an input seismic data in order to deal with the dipping events caused by inaccurate slope estimation. We show the key difference among different types of median filters in detail and demonstrate the principle of the structure-oriented space-varying median filter method. We apply the structure-oriented space-varying median filter method to remove the spike-like blending noise arising from the simultaneous source acquisition. Synthetic and real data examples show that structure-oriented space-varying median filter can significantly improve the signal preserving performance for curving events in the seismic data. The structure-oriented space-varying median filter can also be easily embedded into an iterative deblending procedure based on the shaping regularization framework and can help obtain much improved deblending performance.

A new paper is added to the collection of reproducible documents: Viscoacoustic modeling and imaging using low-rank approximation

A constant-$Q$ wave equation involving fractional Laplacians was recently introduced for viscoacoustic modeling and imaging. This fractional wave equation has a convenient mixed-domain space-wavenumber formulation, which involves the fractional-Laplacian operators with a spatially varying power. We propose to apply low-rank approximation to the mixed-domain symbol, which enables a space-variable attenuation specified by the variable fractional power of the Laplacians. Using the proposed approximation scheme, we formulate the framework of the $Q$-compensated reverse-time migration ($Q$-RTM) for attenuation compensation. Numerical examples using synthetic data demonstrate the improved accuracy of using low-rank wave extrapolation with a constant-$Q$ fractional-Laplacian wave equation for seismic modeling and migration in attenuating media. Low-rank $Q$-RTM applied to viscoacoustic data is capable of producing images comparable in quality with those produced by conventional RTM from acoustic data.

A new paper is added to the collection of reproducible documents: Missing log data interpolation and semiautomatic seismic well ties using data matching techniques

Relating well log data, measured in depth, to seismic data, measured in time, typically requires estimating well log impedance and a time-to-depth relationship using available sonic and density logs. When sonic and density logs are not available, it is challenging to incorporate wells into integrated reservoir studies as the wells cannot be tied to seismic. We propose a workflow to estimate missing well log information, automatically tie wells to seismic data and generate a global well-log property volume using data matching techniques. We first use local similarity scan to align all logs to constant geologic time and interpolate missing well log information. Local similarity is then used to tie available wells with seismic data. Finally, log data from each well is interpolated along local seismic structures to generate global log property volumes. We use blind well tests to verify the accuracy of well-log interpolation and seismic-well ties. Applying the proposed workflow to a 3D seismic dataset with 26 wells achieves consistent and verifiably accurate results.