A new paper is added to the collection of reproducible documents: $Q$-compensated least-squares reverse time migration using lowrank one-step wave extrapolation

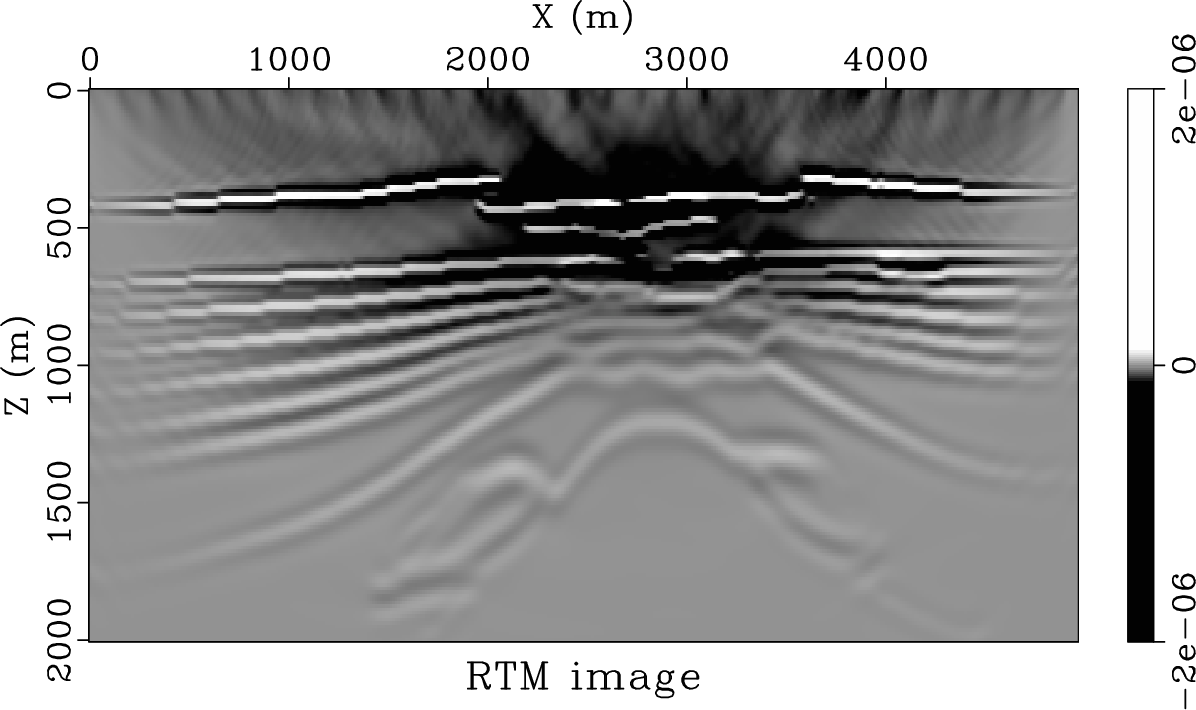
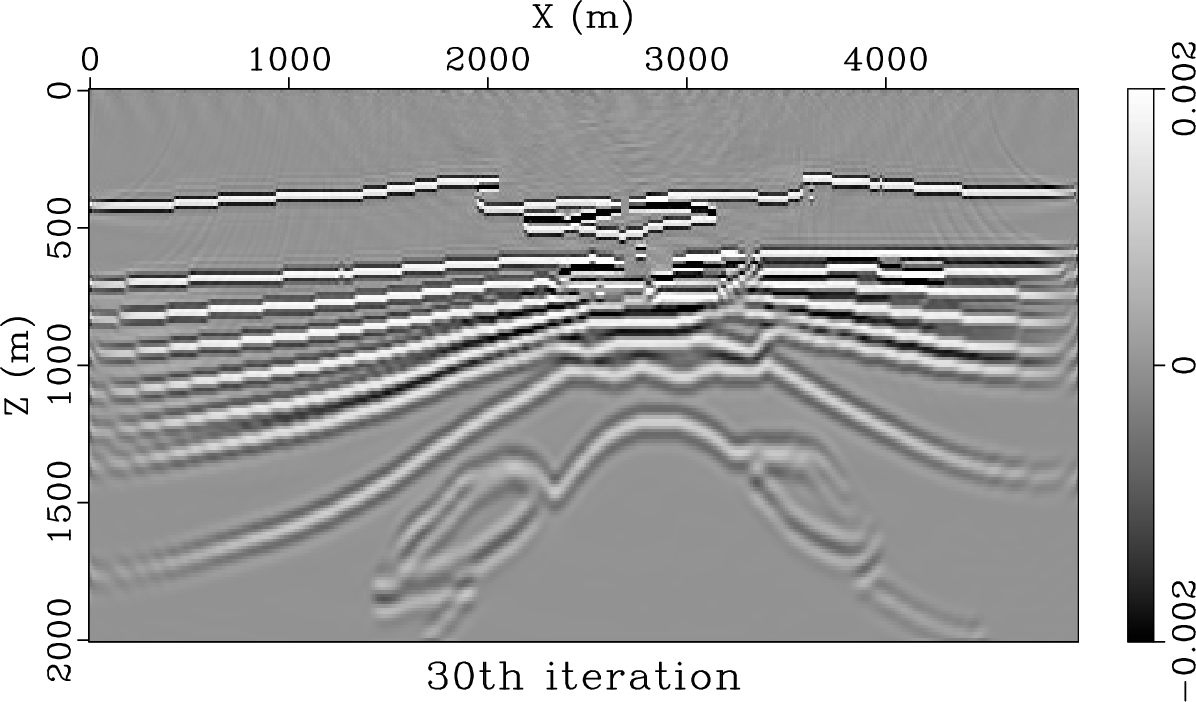
Attenuation of seismic waves needs to be taken into account in order to improve the accuracy of seismic imaging. In viscoacoustic media, reverse time migration (RTM) can be performed with $Q$-compensation, which is also known as $Q$-RTM. Least-squares RTM (LSRTM) has also been shown to be able to compensate for attenuation through linearized inversion. However, seismic attenuation may significantly slow down the convergence rate of the least-squares iterative inversion process without proper preconditioning. We show that incorporating attenuation compensation into LSRTM can improve the speed of convergence in attenuating media, obtaining high-quality images within the first few iterations. Based on the lowrank one-step seismic modeling operator in viscoacoustic media, we derive its adjoint operator using non-stationary filtering theory. The proposed forward and adjoint operators can be efficiently applied to propagate viscoacoustic waves and to implement attenuation compensation. Recognizing that, in viscoacoustic media, the wave equation Hessian may become ill-conditioned, we propose to precondition LSRTM with $Q$-compensated RTM. Numerical examples show that the resulting $Q$-LSRTM method has a significantly faster convergence rate than LSRTM, and thus is preferable for practical applications.