A new paper is added to the collection of reproducible documents:
Accelerated plane-wave destruction
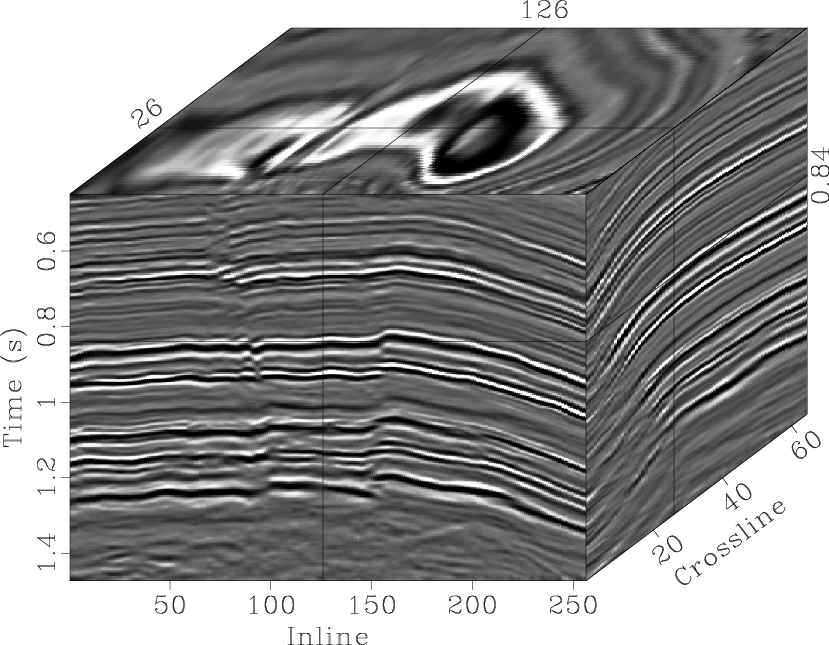
Accelerated PWD
January 30, 2013 Documentation No comments
If I write a research paper using Madagascar, do I need to add a reference?
January 19, 2013 FAQ No comments
Please take into account the following considerations:
- According to the GPL license, there is no legal requirement to reference Madagascar when you use it.
 Please consider contributing your paper to Madagascar. Multiple studies have shown that reproducible papers receive more attention from the readers and make a higher impact. Releasing your paper can also help you maintain your own research results. In words of Jon Claerbout,
Please consider contributing your paper to Madagascar. Multiple studies have shown that reproducible papers receive more attention from the readers and make a higher impact. Releasing your paper can also help you maintain your own research results. In words of Jon Claerbout,
“It takes some effort to organize your research to be reproducible. We found that although the effort seems to be directed to helping other people stand up on your shoulders, the principal beneficiary is generally the author herself. This is because time turns each one of us into another person, and by making effort to communicate with strangers, we help ourselves to communicate with our future selves.”
 If codes from Madagascar played an important role in the research that led to your paper, referencing it is a scientifically ethical thing to do. As stated by the Ethical Guidelines of the American Mathematical Society,
If codes from Madagascar played an important role in the research that led to your paper, referencing it is a scientifically ethical thing to do. As stated by the Ethical Guidelines of the American Mathematical Society,
“The correct attribution of mathematical results is essential, both because it encourages creativity, by benefiting the creator whose career may depend on the recognition of the work and because it informs the community of when, where, and sometimes how original ideas entered into the chain of mathematical thought.”
Of course, such statements can be applied not only to mathematical ideas but also to computational results.
 How to cite Madagascar? Mike Jackson from the Software Sustainability Institute makes a set of clear recommendations for citing software. A citation may look like Madagascar software. Version 1.4. October 2012. https://www.ahay.org/ or more specific with reference to a particular program used and its author. In BibTeX, you can use something like
How to cite Madagascar? Mike Jackson from the Software Sustainability Institute makes a set of clear recommendations for citing software. A citation may look like Madagascar software. Version 1.4. October 2012. https://www.ahay.org/ or more specific with reference to a particular program used and its author. In BibTeX, you can use something like
Program of the month: sfricker1
January 8, 2013 Programs No comments
sfricker1 implements 1-D convolution with the Ricker wavelet.
The following example from rsf/rsf/wedge shows convolution modeling with a wedge model using sfricker1.
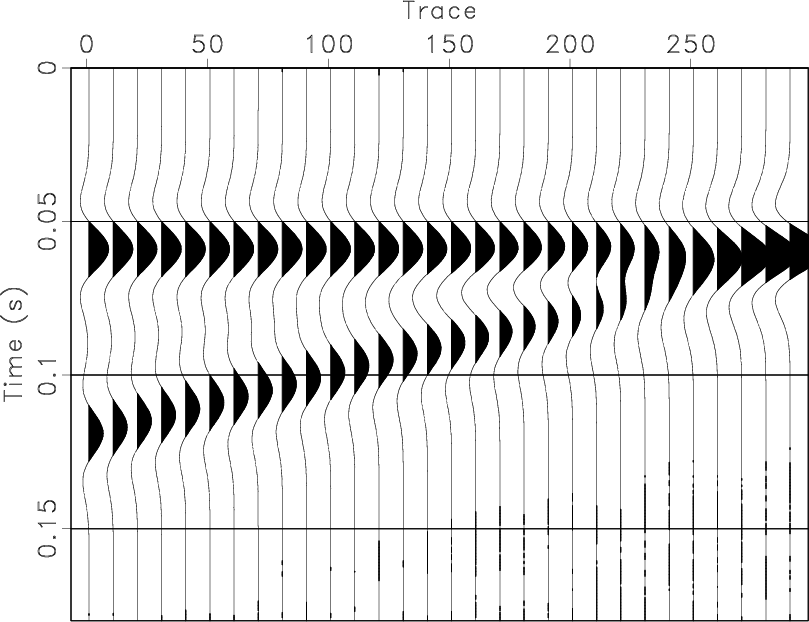
The convolution is implemented in the frequency domain, where the Ricker wavelet takes the form
$$F(\omega) = \frac{\omega^2}{\omega_0^2}\,\exp\left(-\frac{\omega^2}{\omega_0^2}\right)$$
The peak frequency $\omega_0$ can be specified either in hertz (with frequency= parameter) as a fraction of the Nyquist frequency (with freq= parameter). Optionally, it is possible to combine the Ricker wavelet with a half-order derivative filter using deriv=y.